Computer Graphics: Materials
재질 (Materials)
- 이 보고서는 레이 트레이싱 렌더러에서 확산성(diffuse), 금속성(metallic), 유전체(dielectric)와 같은 다양한 재질을 구현하는 기본 개념을 설명합니다.
레이 트레이싱 (Ray Tracing)
- 재질에 대해 자세히 알아보기 전에, 먼저 레이 트레이싱의 핵심 원리를 이해하는 것이 중요합니다.
정방향 대 역방향 경로 추적 (Forward vs. Backward Path Tracing)
- 현실 세계에서 광선은 광원에서 시작하여 장면을 통과하고, 표면에서 반사된 후 관찰자의 눈에 도달합니다.
- 이 과정을 광선 추적(light tracing) 또는 정방향 경로 추적(forward path tracing)이라고 합니다.
- 하지만, 이를 직접 시뮬레이션하는 것은 계산적으로 비효율적입니다.
- 광원에서 방출되는 광선 중 극히 일부만이 카메라에 도달하므로, 계산이 낭비됩니다.
- 정방향 경로 추적은 코스틱(caustics, 빛 모음) 렌더링과 같은 특정 시나리오에서는 효과적일 수 있지만, 대부분의 최신 레이 트레이서는 다른 접근 방식을 사용합니다.
- 역방향 경로 추적(Backward path tracing) (또는 간단히 “경로 추적, path tracing”)은 반대 방향으로 작동합니다.
- 카메라(또는 눈)에서 장면으로 광선을 발사합니다.
- 이 접근 방식은 훨씬 더 효율적입니다.
- 계산된 모든 광선이 화면의 보이는 픽셀에 기여하도록 보장하기 때문입니다.
- 이 모델에서 광선은 카메라 센서의 픽셀에서 장면으로 추적됩니다.
- 광선이 물체와 교차하면, 해당 교차 지점에서 새로운 광선이 산란됩니다.
- 이 과정은 광선이 광원에 도달하거나, 최대 반사 한계에 도달할 때까지 재귀적으로 계속됩니다.
- 광선이 궁극적으로 광원에 도달하면,
- 그 광원의 색상 기여도를 카메라로 되돌려 보내며, 이 값은 광선이 상호작용한 각 표면의 속성에 의해 감쇠됩니다.
- 광선이 광원에 전혀 도달하지 않으면,
- 기본 배경색(대개 검은색)이 할당됩니다.
- 광선이 물체와 교차하면, 해당 교차 지점에서 새로운 광선이 산란됩니다.
확산 반사율 (Diffuse Albedo)
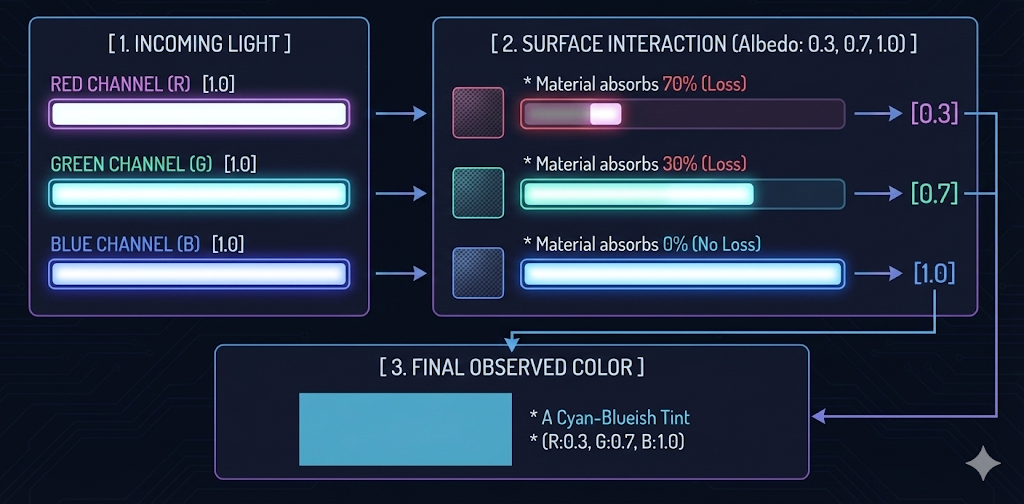
- 확산 반사율(diffuse albedo)은 표면에 입사하는 빛의 백분율 중 표면이 모든 방향으로 균일하게 반사하는 정도를 정의하는 재질 속성입니다.
- 예를 들어, $[0.3, 0.7, 1.0]$의 확산 반사율을 가진 표면은 입사광의 빨간색 성분의 $70\%$, 녹색 성분의 $30\%$, 파란색 성분의 $0\%$를 흡수합니다.
- 확산 반사율에 의해 변조된 나머지 빛이 물체에 색상을 부여합니다.
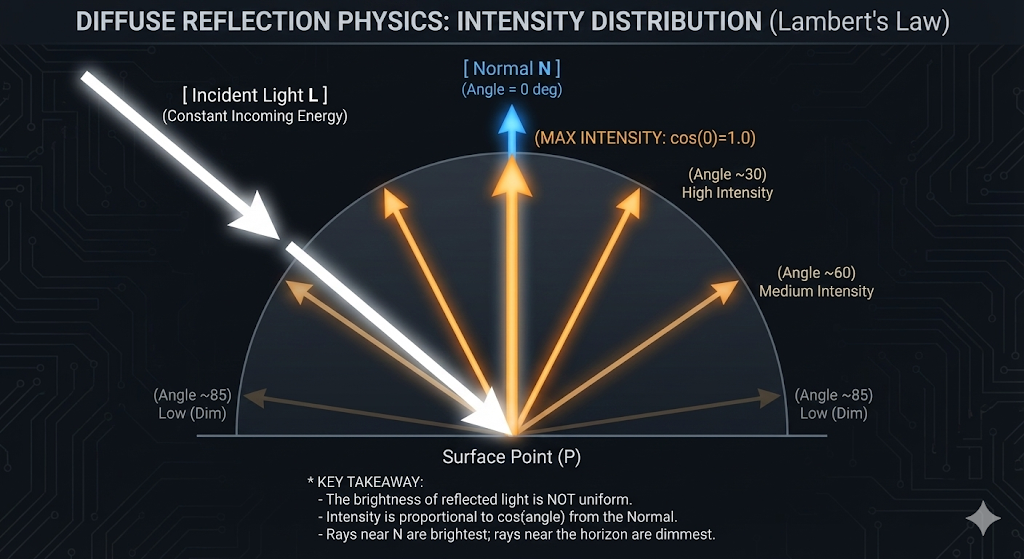
광도 (Light Intensity)
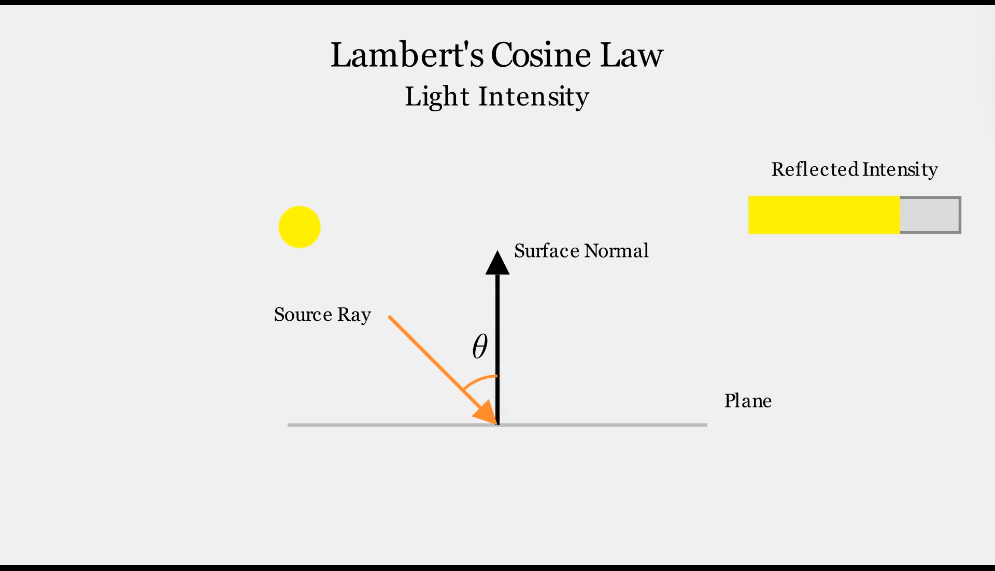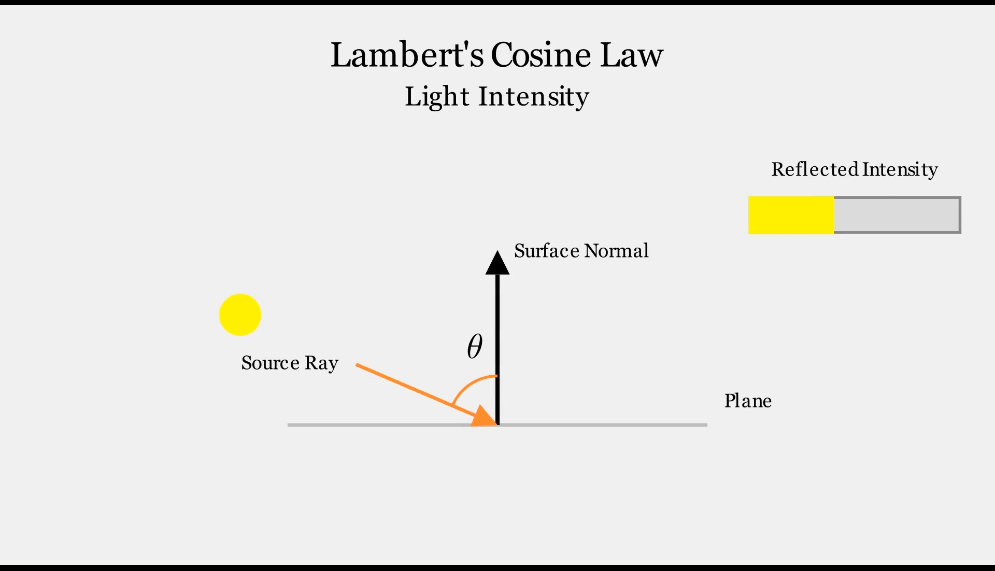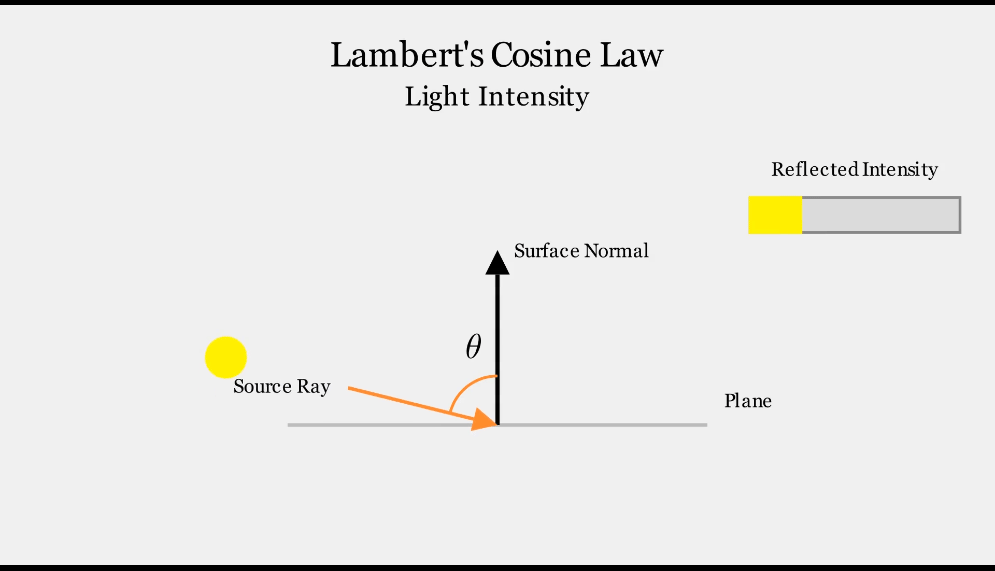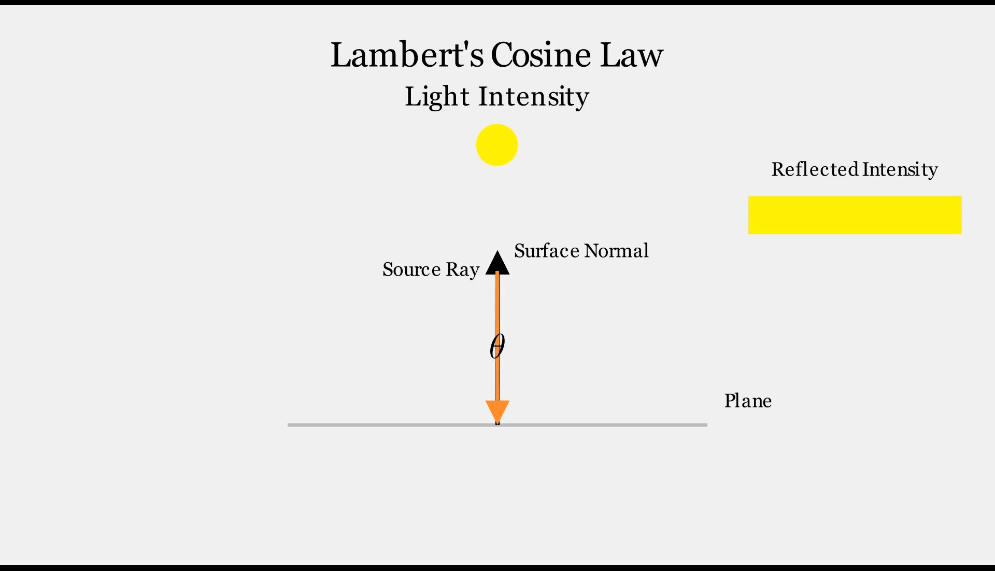
- 표면이 받는 빛의 강도는 표면 법선과 입사 광선 사이의 각도에 따라 달라집니다.
- 광선이 표면 법선과 평행할 때 최대 강도에 도달하며, 각도가 증가함에 따라 감소합니다.
-
이 관계는 Lambert의 코사인 법칙(Lambert’s Cosine Law)에 의해 설명됩니다.
\[I_\text{reflected} = I_\text{original} * cos\theta\]- 각도 $\theta$는 표면 법선과 입사 광선 사이의 각도입니다.
- 강도는 일반적으로 $max(0,cos\theta)$와 같은 함수를 사용하여 음수가 되지 않도록 제한됩니다.
재귀적 계산 (Recursive Calculation)
- 픽셀의 최종 색상을 계산하기 위해, 레이 트레이서는 재귀 함수를 사용합니다.
- 카메라에서 광선이 추적되고, 각 반사에서 색상은 표면 속성과 다음 광선에서 오는 색상의 곱으로 결정됩니다.
-
핵심 재귀 공식은 다음과 같이 일반화될 수 있습니다:
\[\text{color}_{\text{reflected}} = \text{intensity}_{\text{light}} \times \text{albedo}_{\text{current}} \times \text{color}_{\text{incoming}}\]- 이 공식은 일련의 변조(modulations)를 설명합니다.
- 처음에 입사 광선의 색상은 교차된 표면의 확산 반사율(diffuse albedo)과 곱해집니다.
- 이 곱셈은 각 RGB 구성 요소의 흡수 및 반사를 시뮬레이션합니다.
- 그 결과는 입사각에서 파생된 스칼라 값인 광도에 의해 감쇠됩니다.
- 이 연산들의 최종 곱이 반사된 광선의 색상을 결정합니다.
- 재귀는 다음 세 가지 경우 중 하나에서 종료됩니다:
- 광선이 광원에 도달하는 경우
- 재귀가 종료되고 광원의 색상(예: 흰색)이 반환됩니다.
- 광선이 아무것도 맞추지 못하는 경우
- 재귀가 종료되고 배경 또는 스카이박스 색상이 반환됩니다.
- 최대 재귀 깊이에 도달하는 경우
- 광선이 모든 에너지를 잃었다고 가정하고, 함수는 검은색을 반환합니다.
- 이는 무한 루프를 방지하고 계산을 제한하는 중요한 최적화입니다.
- 일반적인 최대 깊이는 5에서 10회 반사 사이입니다.
- 광선이 광원에 도달하는 경우
-
색상 필터링을 보여주는 재귀적 레이 트레이싱 경로 (Recursive Ray Tracing Path Illustrating Color Filtering).
빛의 흡수 및 필터링 (Light Absorption and Filtering)
- 광선의 색상은 일정한 값이 아닙니다.
- 이는 광선이 상호 작용하는 각 표면에서 필터링되는 누적 속성입니다.
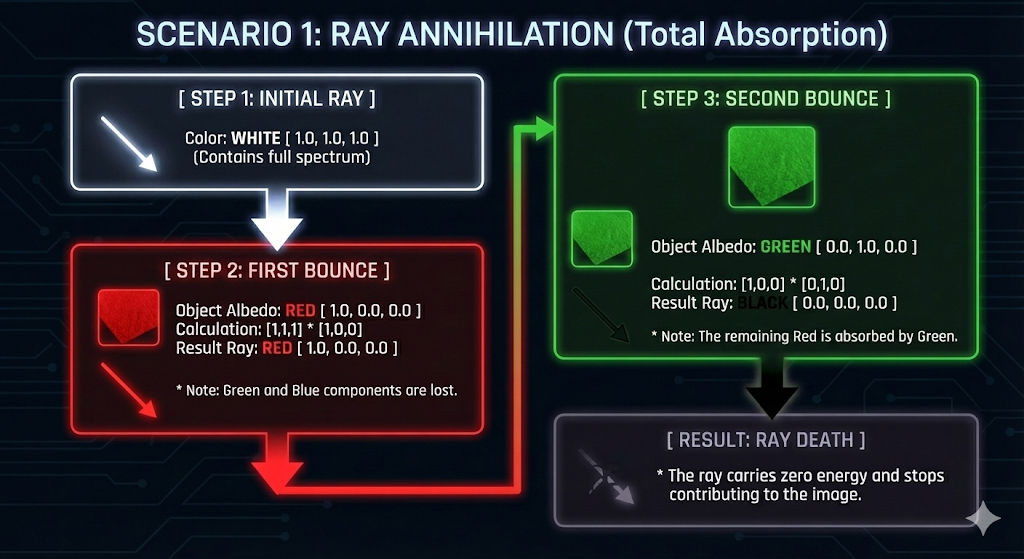
시나리오 1: 광선 소멸 (Ray Annihilation)
- 광선은 색상 구성 요소를 완전히 흡수하는 표면에 의해 필터링되면 효과적으로 “사멸”할 수 있습니다.
- 초기 상태
- 흰색 광선 (RGB = $[1, 1, 1]$)
- 1차 반사 (Bounce 1)
- 광선이 순수한 빨간색 물체(확산 반사율 $[1, 0, 0]$)에 부딪힙니다.
- 광선의 색상은 빨간색이 되며, 녹색 및 파란색 구성 요소를 잃습니다.
- 2차 반사 (Bounce 2)
- 이제 빨간색인 광선이 순수한 녹색 물체(확산 반사율 $[0, 1, 0]$)에 부딪힙니다.
- 물체가 모든 빨간색 빛을 흡수하고, 광선에 남은 녹색 또는 파란색 구성 요소가 없으므로 광선의 색상은 검은색(RGB = $[0, 0, 0]$)이 됩니다.
- 광선은 효과적으로 소멸되며 더 이상 최종 이미지에 기여하지 않습니다.
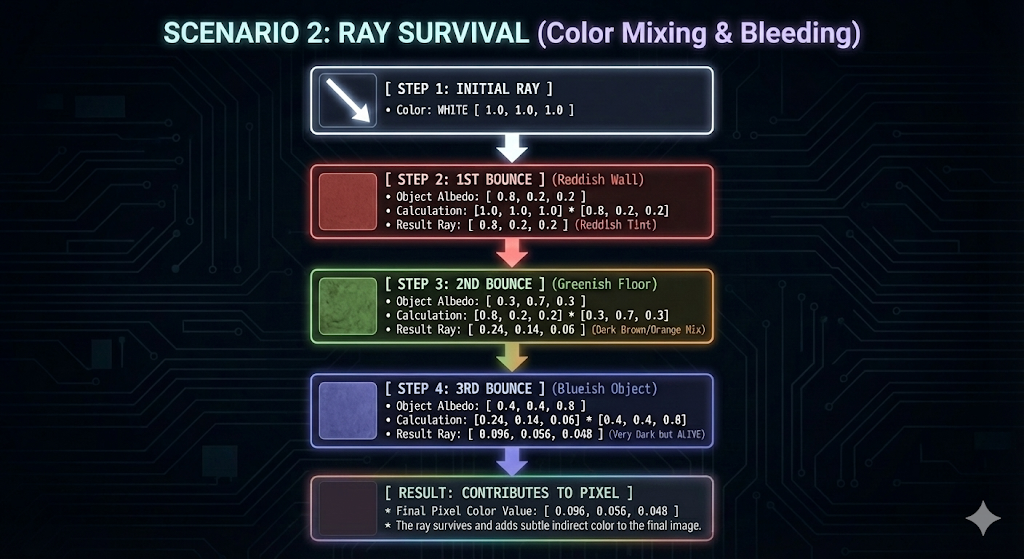
시나리오 2: 광선 생존 (Ray Survival)
- 광선의 색상과 물체의 확산 반사율이 겹치는 색상 구성 요소를 가지면, 광선은 강도가 감소하더라도 여러 번의 반사를 통해 생존할 수 있습니다.
- 이것이 복잡하고 사실적인 색상을 만드는 원리입니다.
- 초기 상태
- 흰색 광선 (RGB = $[1, 1, 1]$).
- 1차 반사 (Bounce 1)
- 붉은 빛이 도는 벽(확산 반사율 $[0.8, 0.2, 0.2]$)에 부딪힙니다.
- 광선은 붉은 빛이 도는 빛이 됩니다.
- 2차 반사 (Bounce 2)
- 푸른 빛이 도는 바닥(확산 반사율 $[0.3, 0.7, 0.3]$)에 부딪힙니다.
- 광선은 더 흐릿하고 혼합된 색상의 빛이 됩니다.
- 3차 반사 (Bounce 3)
- 푸른 빛이 도는 물체(확산 반사율 $[0.4, 0.4, 0.8]$)에 부딪힙니다.
- 광선의 최종 색상은 매우 흐릿하고 혼합된 색상의 빛입니다.
- 초기 상태
-
최종 픽셀 값은 이 모든 색상 필터링 상호 작용의 누적 결과이며, 이것이 단일 광선의 장면 통과 경로가 최종 픽셀의 색상을 결정하는 이유입니다.
표면 형상의 이중성: Micro/Macro Space
- 렌더링에서 표면의 동작은 보는 스케일에 따라 다르게 해석됩니다.
-
이 이중성은 정확한 쉐이딩의 기본입니다.
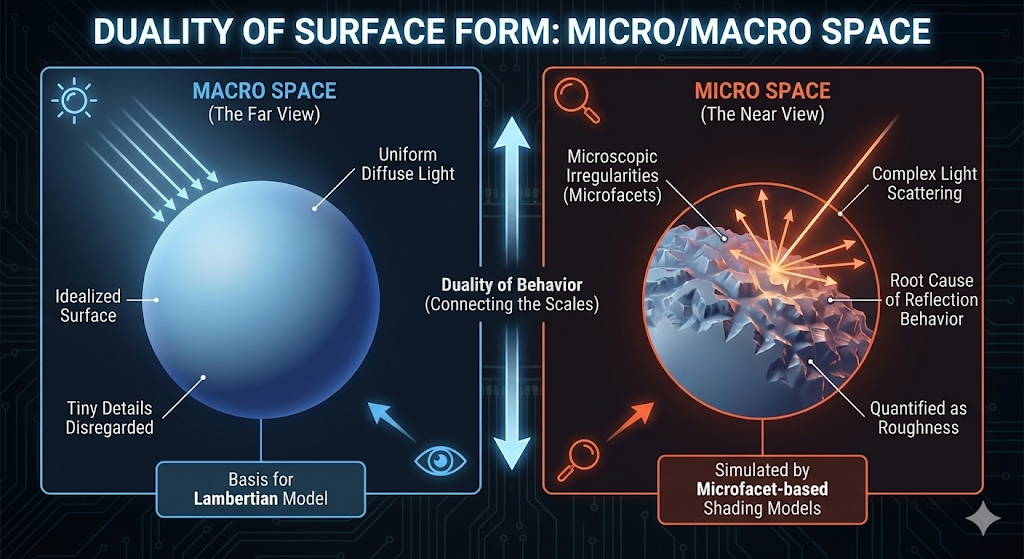
거시 공간 (Macro Space, The Far View)
- 정의: 먼 거리에서 볼 때의 표면 모습(거시 공간)을 나타냅니다.
- 동작: 표면은 확산광(Diffuse Light)에 의해 균일하게 조명된 것처럼 보입니다.
- 모델링: 이 관점은 표면의 미세한 디테일이 무시되는 Lambertian 모델과 같은 이상적인 쉐이딩 모델의 기반을 형성합니다.
미시 공간 (Micro Space, The Near View)
- 정의: 가까운, 미시적 수준에서 볼 때의 실제 표면(미시 공간)을 나타냅니다.
- 동작: 물리적 표면은 미세한 불규칙성(Microscopic Irregularities) 또는 미세 면(Microfacets)을 가집니다.
- 이 미세한 요철들이 빛을 예측 불가능하게 산란(Scattering)시키는 근본 원인이 됩니다.
- 표현: 이 산란 행동은 정량화되어 재질의 거칠기(Roughness)로 표현됩니다.
- 의의: 정확하고 사진처럼 사실적인 렌더링은 복잡한 미세 면 기반 쉐이딩 모델(Microfacet-based shading models)을 사용하여 이러한 미시적 불규칙성을 시뮬레이션해야 합니다.
- 이러한 고급 모델은 빛 반사를 정확하게 예측하기 위해 이 미세한 면들의 통계적 방향과 기하학적 구조를 고려합니다.
레이 트레이싱에서의 반사 (Reflection in Ray Tracing)
- 레이 트레이싱은 광선의 경로를 계산하여 빛이 표면과 상호 작용하는 방식을 시뮬레이션합니다.
- 광선이 물체에 부딪힐 때의 동작은 물체의 재질 속성에 따라 달라집니다.
- 이 섹션은 세 가지 기본 반사 모델의 구현을 자세히 설명합니다:
- 확산성 (Lambertian)
- 정반사 (금속)
- 그리고 이 둘의 조합 (Fuzzy Reflection).
확산성 (Lambertian) 반사 (Diffuse Reflection)
- 확산 반사(Diffuse Reflection)는 무광택(matte), 비광택 표면의 특징입니다.
- 메커니즘 (Mechanism): 표면에 도달한 빛은 표면의 미세한 불규칙성(Microscopic Irregularities) 때문에 표면의 모든 방향으로 균일하게 산란됩니다. 이상적인 Lambertian 표면은 관찰 시점과 무관하게 동일한 밝기로 보입니다.
- 조명 세기 (Illumination Intensity): 표면의 밝기는 Lambert의 코사인 법칙에 의해 정의된 대로 입사광과 법선 사이 각도의 코사인 값에 비례합니다.
- 정확한 확산 반사를 시뮬레이션하고 렌더링 방정식(Rendering Equation)을 풀기 위해, 레이 트레이싱은 몬테카를로 방법을 기반으로 한 코사인 가중 반구 샘플링(Cosine-Weighted Hemisphere Sampling)을 사용합니다.
- 가중치 부여 (Weighting): 이 기법은 새로운 반사 광선이 표면 법선 ($\vec{n}$) 방향에 가까울수록 더 높은 확률 (더 큰 가중치)을 갖도록 샘플을 생성합니다.
- 효율성 (Efficiency): 이는 법선 근처의 광선이 전체 장면 조명에 더 많이 기여하므로, 해당 영역에 샘플을 집중시켜 이미지의 노이즈(Noise)를 줄이고 계산 효율성을 크게 향상시킵니다.
- 구현 세부 단계 (Implementation Steps):
- 임의 벡터 생성 및 단위 구 정규화 (Arbitrary Vector Generation and Unit Sphere Normalization):
- [−1,1] 범위에서 임의의 $(\mathbf{x}, \mathbf{y}, \mathbf{z})$ 좌표가 생성됩니다.
- 이 벡터는 정규화되어 단위 구(Unit Sphere) 표면 위의 임의 방향 벡터 ($\vec{v}_{\text{rand}}$)를 생성합니다.
- (안정성에 대한 참고): 중심에 너무 가까운 점은 수치적 안정성을 보장하기 위해 기각됩니다.
- 반구 제약 조건 검사 (Hemisphere Constraint Check):
- 반사 광선은 표면 법선 $\vec{n}$이 정의하는 반구(Hemisphere) 내에 있어야 합니다.
- 이 제약 조건은 법선 $\vec{n}$과 생성된 벡터 $\vec{v}_{\text{rand}}$ 사이의 내적(Dot Product)을 확인하여 검증됩니다.
- 방향 조정 (Direction Correction):
- 내적 값이 음수인 경우 (광선이 표면 내부로 향함을 나타냄), 무작위로 생성된 방향 벡터는 역전됩니다 (음수 부호를 적용하여 방향이 반전됨).
- 이는 광선이 필요한 반구 내, 즉 표면 바깥쪽으로 향하도록 강제합니다.
- 임의 벡터 생성 및 단위 구 정규화 (Arbitrary Vector Generation and Unit Sphere Normalization):
-
이 체계적인 절차는 계산적으로 효율적이며 물리적으로 타당한 확산 반사를 생성합니다.
정반사 (금속) 반사 (Specular (Metal) Reflection)
- 정반사는 빛이 산란되지 않고 단일하고 예측 가능한 방향으로 반사되는, 광택 있고 거울 같은 표면에서 발생합니다.
- 반사의 법칙은 입사각과 반사각이 같다고 명시합니다.
-
완벽하게 반사된 광선의 방향은 벡터 수학에서 파생된 다음 공식을 사용하여 계산할 수 있습니다:
\(v_\text{reflected}=v_\text{incident}−2(v_\text{incident}\cdot n)n\)
- 여기서:
- $v_{incident}$는 정규화된 입사 광선 벡터입니다.
- $n$은 교차점에서 정규화된 표면 법선 벡터입니다.
-
내적 ($v_{incident}\cdot n$)은 입사 벡터의 법선에 대한 올바른 투영을 보장하며, 이는 반사 방향을 결정하는 데 중요합니다.
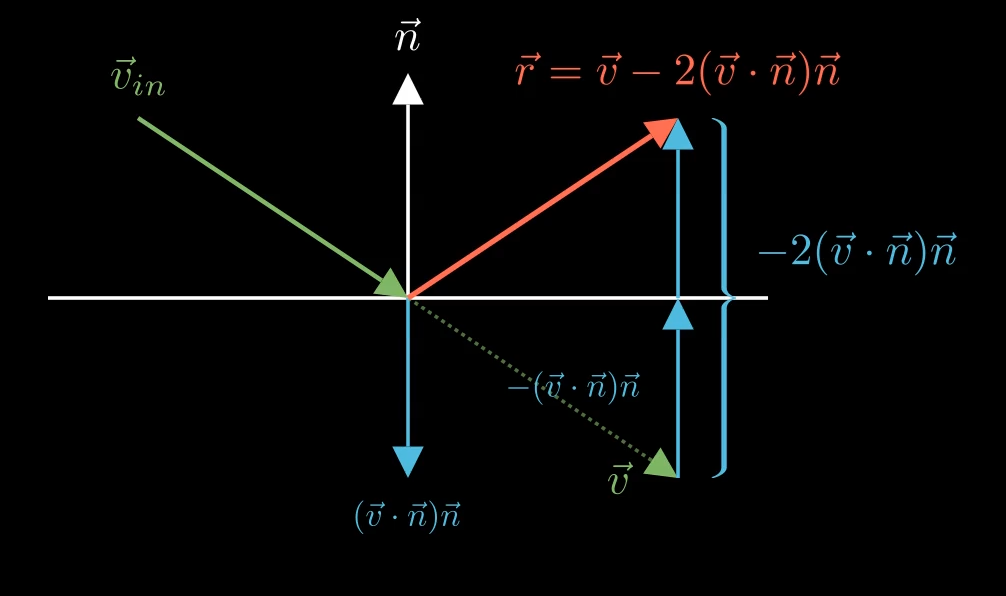
- 여기서:
- 내적이 반사 방향을 올바르게 결정하려면, 입사 벡터와 법선 벡터가 모두 표면에서 멀어지거나, 모두 표면을 향해야 한다는 것이 필수적입니다.
- 일관된 계산을 위해 입사 광선 방향(표면을 향함)과 반전된 법선 벡터를 사용하는 것이 표준 관행입니다.
-
Click to see the code
inline Vec3 getReflectedMirror(const Vec3& inputVector, const Vec3 &unitVector) { return inputVector - 2 * performDot(inputVector, unitVector) * unitVector; }
퍼지 반사 (Fuzzy Reflection)
- 퍼지 반사(Fuzzy reflection)는 브러시 처리되거나 긁힌 금속과 같이 완벽하게 광택이 나지 않는 금속 표면을 시뮬레이션하기 위한 모델입니다.
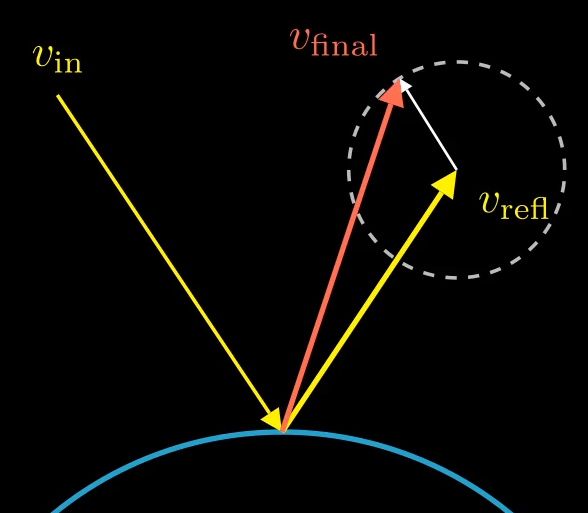
- 이 모델은 정반사 방향 주변으로 반사된 광선을 산란시켜 정반사에 어느 정도의 무작위성을 도입합니다.
- 이 효과는 완벽하게 반사된 광선 벡터에 작은, 무작위적인 섭동(perturbation)을 추가함으로써 달성됩니다.
- 이 섭동의 크기는 퍼지니스 매개변수(fuzziness parameter)에 의해 제어되며, 이는 이상적인 반사 벡터의 끝점을 중심으로 하는 구의 반경을 효과적으로 나타냅니다.
- 산란된 광선에 대한 공식은 다음과 같습니다:
\(v_\text{scattered}=v_\text{unit_reflected}+f_\text{fuzziness}\cdot v_{\text{random}}\)
- 여기서:
- $v_\text{unit_reflected}$는 정규화된, 완벽하게 반사된 벡터입니다.
- $f_\text{fuzziness}$는 스칼라 퍼지니스 매개변수입니다.
- $v_\text{random}$은 무작위 단위 벡터입니다.
- 여기서:
- 중요한 구현 세부 사항은 산란된 광선의 방향이 표면 바깥쪽을 향하도록 보장하는 것입니다.
- 산란된 벡터와 표면 법선 사이의 내적을 사용하여 물체 내부로 다시 산란되는 광선을 흡수하는 간단한 확인을 수행할 수 있습니다.
-
Click to see the code
class Metal : public Material { public: Metal(const Color& inputAlbedo, double inputFuzz) : albedo(inputAlbedo), fuzz(inputFuzz) { if (inputFuzz < -1) inputFuzz = -1; else if (inputFuzz > 1) inputFuzz = 1; } bool doesScatter(const Ray &inputRay, const HitRecord &record, Color &attenuation, Ray &scatteredRay) const override { Vec3 reflectedVector = getReflectedMirror(inputRay.getDirection(), record.normalizedVector); reflectedVector = getUnitVector(reflectedVector) + (fuzz * getRandomUnitVector()); scatteredRay = Ray(record.hitPosition, reflectedVector); attenuation = albedo; return (performDot(scatteredRay.getDirection(), record.normalizedVector) > 0); } private: Color albedo; double fuzz; };
굴절: 유전체에서의 빛의 행동 (Refraction: The Behavior of Light in Dielectrics)
- 광선이 유전체(dielectric), 즉 유리, 물, 다이아몬드와 같은 투명한 재질을 만나면, 일반적으로 두 가지 구성 요소로 분할됩니다:
- 반사된 광선(reflected ray)
- 그리고 굴절된 (투과된) 광선(refracted (transmitted) ray).
- 반사된 광선은 표면에서 “튀어 나가”는 반면, 굴절된 광선은 빛의 속도 변화로 인해 경로를 구부리며 재질 내부로 통과합니다.
굴절률 (Refractive Index, n) 및 스넬의 법칙 (Snell’s Law)
-
재질의 굴절률($n$)은 빛이 재질을 통과할 때 얼마나 많이 구부러지는지를 정량화하는 무차원 물리 상수입니다.
-
이는 진공에서의 빛의 속도($c$)와 매질에서의 빛의 속도($v$)의 비율로 정의됩니다: \(n={c\over v}\)
- 두 매질의 굴절률과 광선의 각도 사이의 관계는 스넬의 법칙(Snell’s Law)에 의해 지배됩니다:
\(n_1sin\theta_1=n_2sin\theta_2\)
- 여기서 $\theta_1$과 $\theta_2$는 각각 표면 법선으로부터 측정된 입사 광선과 굴절 광선의 각도입니다.

- 여기서 $\theta_1$과 $\theta_2$는 각각 표면 법선으로부터 측정된 입사 광선과 굴절 광선의 각도입니다.
- 빛이 더 조밀한 매질($n_1 < n_2$)로 들어갈 때,
- 속도가 느려지고 법선 쪽으로 구부러집니다.
- 반대로, 빛이 덜 조밀한 매질($n_1 > n_2$)로 들어갈 때,
- 속도가 빨라지고 법선에서 멀어집니다.
- 이 법칙은 현실적인 투명 물체를 렌더링하는 데 필수적인, 레이 트레이싱에서 굴절된 광선의 방향을 계산하기 위한 기본입니다.
굴절 벡터 계산 (Calculating the Refracted Vector)
- 굴절된 광선의 방향은 입사 광선 벡터를 표면 법선에 평행한 성분과 수직인 성분으로 분해하여 유도할 수 있습니다.
- 입사 단위 벡터 $a$, 단위 법선 벡터 $n$, 굴절 단위 벡터 $b$에 대해:
\(b = \frac{n_1}{n_2} (a - (a \cdot n) n) - \sqrt{1 - (\frac{n_1}{n_2})^2 (1 - (a \cdot n)^2)} \cdot n\) -
Click to see the full derivation
- 굴절된 광선의 방향은 스넬의 법칙을 기반으로 한 벡터 접근 방식을 사용하여 수학적으로 유도될 수 있습니다.
- 핵심은 입사 및 굴절 벡터를 표면 법선에 평행한 성분과 수직인 성분으로 분해하는 것입니다.
- 벡터를 정의해 봅시다:
- $a$: 정규화된 입사 광선 벡터.
- $n$: 정규화된 표면 법선 벡터.
- $b$: 정규화된 굴절 광선 벡터.
- $\theta_1$: 입사 광선과 법선 사이의 각도.
- $\theta_2$: 굴절 광선과 법선 사이의 각도.
-
입사 및 굴절 벡터는 다음과 같이 분해될 수 있습니다: \(a=a_{\parallel} + a_{\perp}\)
\(b=b_{\parallel} + b_{\perp}\)
- 수직 성분의 크기는 스넬의 법칙과 관련이 있습니다.
-
벡터와 법선에 의해 정의된 각도를 사용할 수 있습니다. \(sin\theta_1= ||a_{\perp}||\)
\(sin\theta_2= ||b_{\perp}||\)
-
-
스넬의 법칙은 벡터 형식으로 다음과 같이 표현될 수 있습니다: \(n_1sin\theta_1=n_2sin\theta_2\)
\(n_1||a_{\perp}|| =n_2||b_{\perp}||\)
-
벡터 $a_{\perp}$와 $b_{\perp}$가 서로 평행하고 $n$에 수직이라는 점을 감안할 때, 다음과 같이 쓸 수 있습니다: \(b_{\perp} = {n_1 \over n_2}a_{\perp}\)
- 입사 벡터의 수직 성분 $a_{\perp}$는 전체 벡터에서 평행 성분을 빼서 찾을 수 있습니다.
-
평행 성분은 $a$의 $n$에 대한 투영입니다. \(a_{\parallel} = (a\cdot n)n\)
\(a_{\perp} = a- a_{\parallel} =a-(a\cdot n)n\)
-
- 이를 $b_{\perp}$에 대한 방정식에 대입하면: \(b_{\perp} = {n_1 \over n_2}(a-(a\cdot n)n)\)
- 굴절 벡터의 평행 성분 $b_{\parallel}$는 그 크기와 방향으로부터 결정될 수 있습니다.
-
$b$는 단위 벡터이므로, 그 성분들은 피타고라스의 정리를 만족해야 합니다: \(||b||^2 = ||b_{\parallel}||^2 + ||b_{\perp}||^2\)
\[1 = ||b_{\parallel}||^2 + ||b_{\perp}||^2\]
-
-
평행 성분의 크기에 대해 풀면: \(||b_{\parallel}|| = \sqrt{1 - ||b_{\perp}||^2}\)
- 평행 성분의 방향은 법선 벡터의 반대이므로, $-n$으로 표현될 수 있습니다.
- 따라서 평행 성분은 다음과 같습니다: \(b_{\parallel}=||b_{\parallel}|| \cdot (-n) = -\sqrt{1 - ||b_{\perp}||^2}\cdot n\)
-
평행 성분과 수직 성분을 결합하면, 굴절 벡터 $b$에 대한 최종 공식을 얻습니다: \(b=b_{\perp} + b_{\parallel}\)
\[b= {n_1 \over n_2}(a-(a\cdot n)n)\ -\sqrt{1 - ({n_1 \over n_2})^2(1-(a\cdot n)^2)}\cdot n\] - 이 공식은 투명한 재질을 통과하는 빛의 경로를 시뮬레이션하는 데 필수적이며, 모든 물리 기반 레이 트레이싱 엔진의 핵심 구성 요소입니다. </details>
- 굴절된 광선의 방향은 스넬의 법칙을 기반으로 한 벡터 접근 방식을 사용하여 수학적으로 유도될 수 있습니다.
- 이 계산의 핵심 고려 사항은 표면 법선의 방향입니다.
- 이 공식이 유효하려면 입사 벡터와 법선 벡터가 서로 반대 방향을 가리켜야 합니다(예: 하나는 안쪽, 하나는 바깥쪽).
- 광선이 볼륨을 빠져나갈 때, 이 일관성을 유지하기 위해 법선 벡터를 반전해야 합니다.
반사율 및 프레넬 방정식 (Reflectance and Fresnel’s Equations)
- 굴절 외에도 빛의 일부는 표면에서 반사됩니다.
- 반사율(Reflectance)은 반사되는 빛의 백분율입니다.
- 이 값은 프레넬 방정식(Fresnel’s equations)에 의해 설명된 대로 입사각에 따라 달라집니다.
- 이 복잡한 방정식은 두 재질의 굴절률과 입사각을 기반으로 반사율을 정확하게 계산합니다.
슐릭 근사 (Schlick’s Approximation)
- 프레넬 전체 방정식의 계산 복잡성으로 인해, 실시간 렌더링에서 슐릭 근사(Schlick’s approximation)로 알려진 일반적이고 매우 효과적인 단순화가 사용됩니다.
-
이 근사법은 프레넬 방정식을 사용하여 $\theta = 0$ (최소 반사율)일 때의 반사율을 계산하기 쉽다는 사실을 기반으로 반사율 $R(\theta)$을 계산합니다.
\[R_0 = \left({n_1 - n_2 \over n_1+n_2 }\right)^2\]- 이 특수한 경우를 수직 입사(normal incidence)라고 합니다.
-
그런 다음, 이 공식은 주어진 각도 $\theta$를 기반으로 반사율을 근사화하는 데 활용됩니다.
\(R(\theta)=R_0+(1−R_0)(1−cos\theta)^5\) -
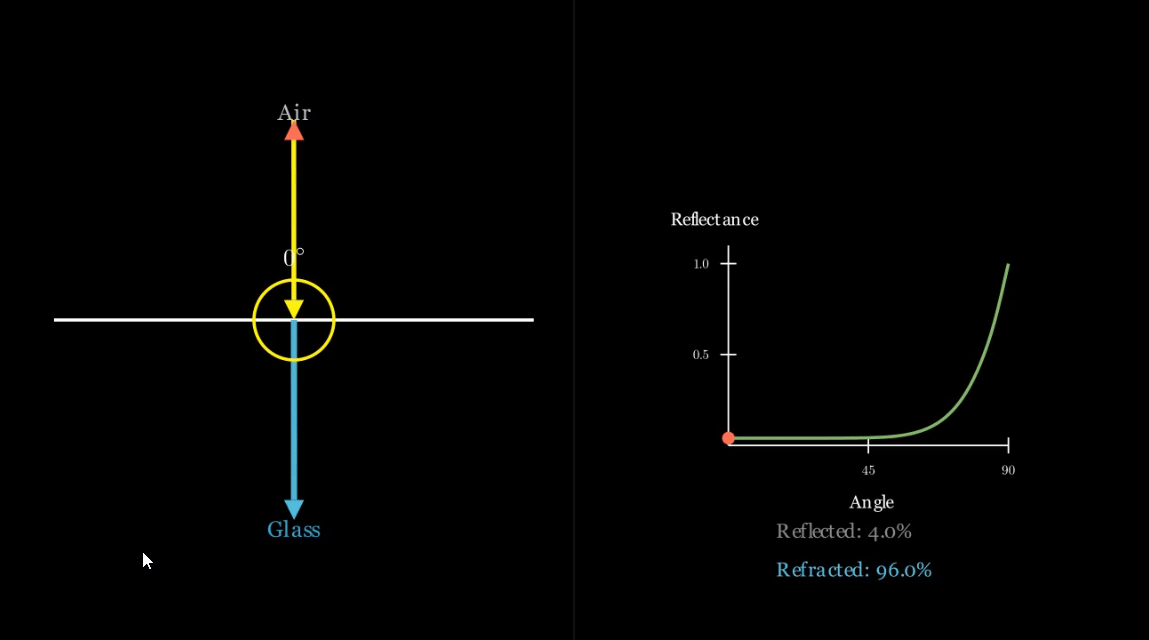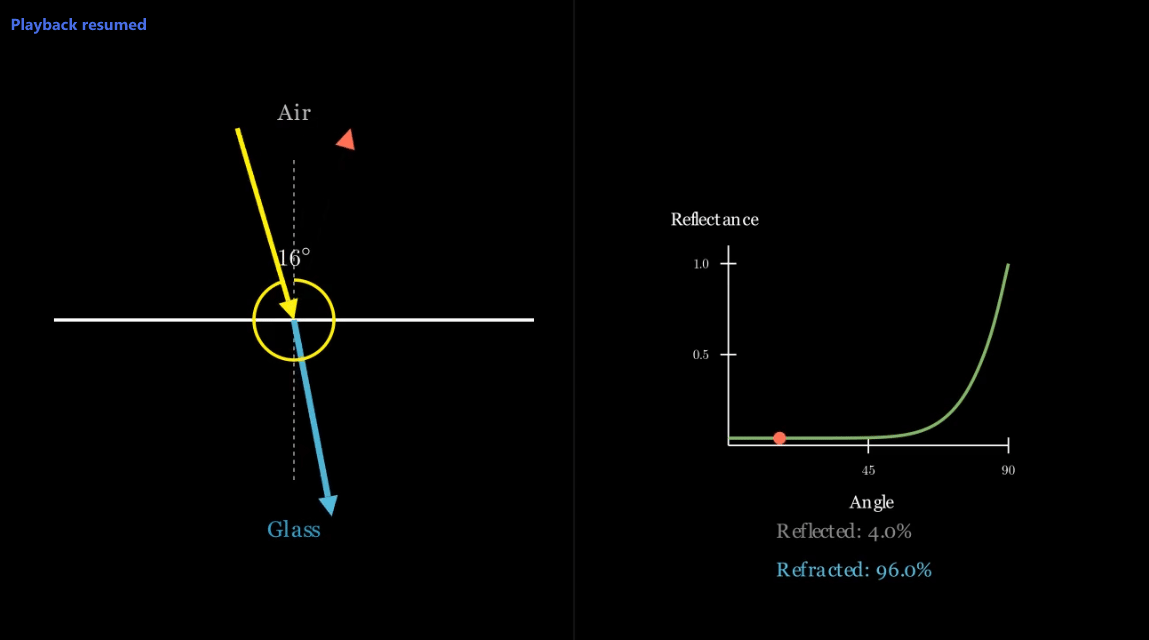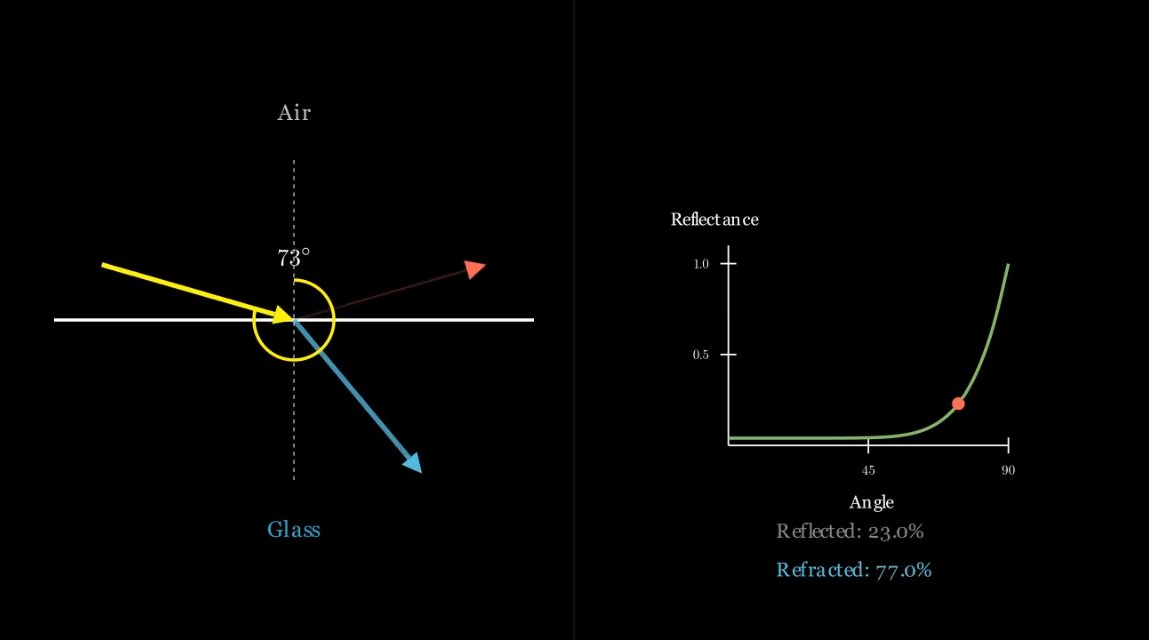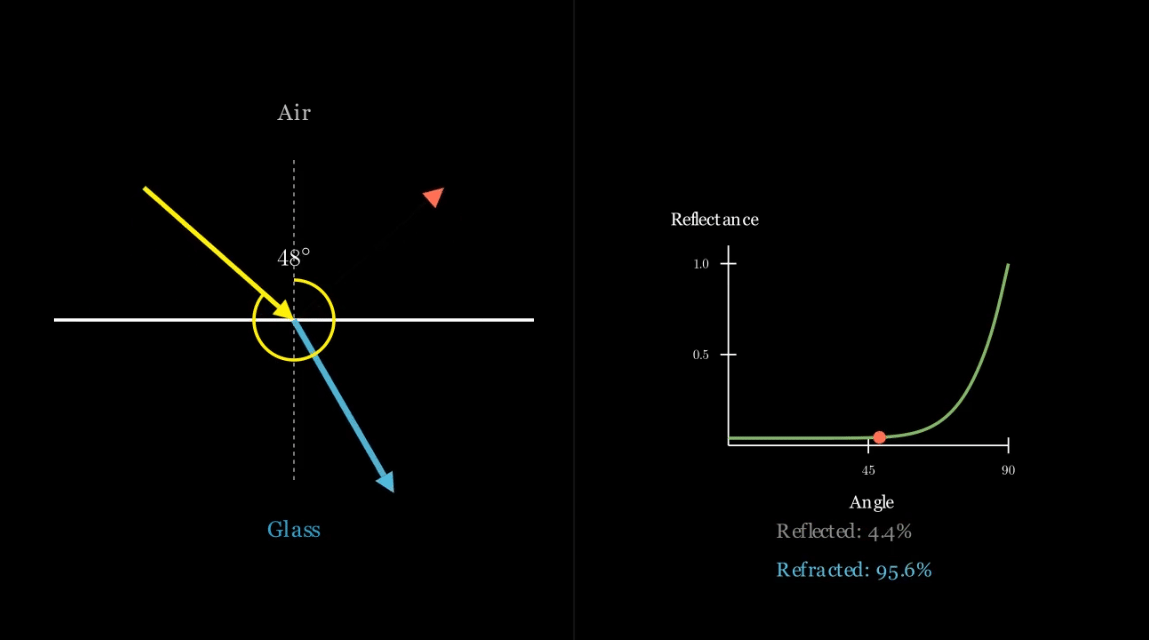
이 근사법은 입사각이 $\pi \over 2$ (극단적인 각도, grazing angle)에 접근할수록 반사율이 급격히 증가함을 보여주는데, 이는 표면에서 종종 “섬광(glint)”이나 “반짝임(glitter)”으로 관찰되는 물리적으로 정확한 행동입니다.
레이 트레이싱에서의 기술적 구현 (Technical Implementation in Ray Tracing)
- 레이 트레이싱의 경우, 반사된 광선 또는 굴절된 광선을 생성할지 여부의 결정은 반사율 값 $R(\theta)$을 기반으로 하는 확률적입니다.
- 난수가 생성되며, 이 난수가 $R(\theta)$보다 작으면 반사된 광선이 추적됩니다.
- 그렇지 않으면 굴절된 광선이 추적됩니다.
- 이 확률적 접근 방식은 빛 분할 현상을 올바르게 시뮬레이션합니다.
실시간 렌더링의 산업 관행 (Industry Practices in Real-Time Rendering)
- 실시간 렌더링에서는 슐릭 근사조차도 계산 비용이 많이 들 수 있습니다.
- 따라서 언리얼 엔진과 같은 많은 게임 엔진은 대부분의 비금속 재질에 대해 상수, 미리 정의된 반사율 값(예:
0.4)을 사용합니다. - 이 접근 방식은 매우 효율적이며 아티스트에게 재질의 시각적 속성을 제어하는 간단한 방법을 제공합니다.
- 따라서 언리얼 엔진과 같은 많은 게임 엔진은 대부분의 비금속 재질에 대해 상수, 미리 정의된 반사율 값(예:
- 완전한 프레넬 계산보다 물리적으로 덜 정확하지만, 성능과 시각적 품질 사이에서 매력적인 절충안을 제공합니다.
Leave a comment