Cause and Effect: the words which explain everything

English

카메라 (Camera)

  • 이 보고서는 물리적 세계와 컴퓨터 그래픽스 영역 모두에서 카메라 작동의 기본 원칙을 설명합니다.
  • 빛의 수렴과 초점 맞추기부터 디포커스 블러(defocus blur) 및 안티앨리어싱(anti-aliasing)과 같은 시각 효과 구현에 이르는 개념을 다룹니다.

카메라 기본 축 구성 (Constructing the Camera’s Basis Axes)

  • 3D 그래픽스에서 카메라의 로컬 좌표계는 세 개의 직교 기본 벡터로 정의됩니다.
  • 이 벡터들은 월드 공간에서 카메라의 방향과 일치하도록 구성되어, 3D 물체를 2D 뷰포트(viewport)에 올바르게 투영할 수 있게 합니다.
  • 이 과정은 세 가지 핵심 매개변수에 의존합니다:
    • 카메라의 위치 (lookfrom)
    • 카메라가 조준하는 지점 (lookat)
    • 월드 공간의 up vector (상향 벡터)

카메라 로컬 축 정의 (Defining the Camera’s Local Axes)

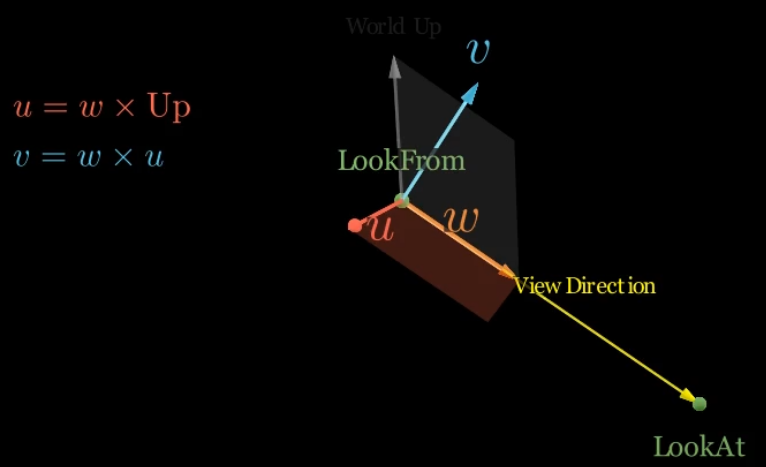
  • 카메라의 로컬 축(일반적으로 u-v-w 기본 축 또는 오른쪽-위-뷰(right-up-view) 기본 축이라고 함)은 벡터 연산을 사용하여 계산할 수 있습니다:
    1. 뷰 방향 (w-축)
      • 첫 번째 축은 카메라의 뷰 방향입니다.
        • 이는 lookfrom 위치에서 lookat 지점을 향하는 벡터입니다.
      • 적절한 기본 벡터를 형성하려면 정규화되어야 합니다.
        • $w=\text{unit_vector}(\text{lookfrom}−\text{lookat})$
      • 벡터는 lookfrom - lookat으로 정의되어 w-축이 장면에서 멀어지는 방향을 가리키도록 보장하며, 이는 컴퓨터 그래픽스에서 자주 사용되는 왼손 좌표계의 표준 관례입니다.
    2. 오른쪽 벡터 (u-축)
      • 두 번째 축, 즉 “오른쪽” 벡터는 뷰 방향과 월드 공간의 상향 벡터 모두에 수직입니다.
        • 이는 외적(cross product)을 사용하여 계산됩니다.
      • 월드 공간의 상향 벡터는 일반적으로 $(0,1,0)$이지만, 계산에 이 벡터의 정규화된 버전을 사용하는 것이 중요합니다.
        • $u=\text{unit_vector}(\text{up_vector}\times w)$
    3. 보정된 상향 벡터 (v-축)
      • 세 번째 축은 카메라 로컬 공간의 “상향” 벡터입니다.
        • 이는 뷰 방향과 오른쪽 벡터 모두에 완벽하게 직교해야 합니다.
      • 초기 상향 벡터가 제공되지만, 이 직교성을 보장하기 위해 새롭고 보정된 상향 벡터가 생성됩니다.
        • 이 역시 외적을 사용하여 계산됩니다.
        • $v=w\times u$
      • 외적에서 벡터의 순서는 오른손 또는 왼손 좌표계에 매우 중요합니다.
        • 위에 표시된 순서는 $u$의 초기 유도에 사용된 왼손 시스템과 일치합니다.     camera_axes

정규화의 중요성 (The Importance of Normalization)

  • 두 개의 직교 단위 벡터의 외적은 이론적으로 다른 단위 벡터를 생성하지만, 실제로는 항상 그런 것은 아닙니다.
    • 부동 소수점 산술의 한계로 인해 계산된 크기가 1에서 약간 벗어날 수 있습니다.
  • 따라서 각 외적 연산 후에 결과 벡터를 정규화하는 것은 표준적이며 필수적인 관행입니다.
    • lookfrom 및 lookat 지점이 방향을 정의하지만, 빼기와 외적 연산에서 발생하는 결과 벡터의 크기는 다양할 수 있습니다.
    • 정규화는 각 기본 벡터가 단위 길이를 갖도록 보장하며, 이는 일관되고 안정적인 좌표계의 기본 요구 사항입니다.

  • 이 과정은 반복되는 벡터 계산에서 축적될 수 있는 정밀도 오류를 완화하는 데 중요합니다.

    normalization

카메라가 이미지를 형성하는 방식 (How a Camera Forms an Image)

이미지 포인트와 이미지 평면 (Image Point and Image Plane)

  • 카메라는 물체에서 오는 광선을 센서에 수렴시켜 이미지를 형성합니다.
    • 물체는 여러 방향으로 빛을 반사하지만, 카메라 렌즈는 이 광선들을 이미지 평면(Image Plane)이라고 알려진 2D 표면의 단일 지점, 즉 이미지 포인트(Image Point)로 초점을 맞춥니다.
    • 총체적으로 이 지점들은 센서에 반전된 이미지를 형성합니다.
  • 컴퓨터 그래픽스에서 뷰포트(viewport)는 3D 장면이 렌더링되는 화면의 2D 창입니다.
    • 이는 최종 렌더링된 이미지를 나타내며, 물리적 이미지 평면의 디지털 등가물로 간주될 수 있습니다.

    viewport

착란원 (Circle of Confusion, CoC)

  • 물체 위의 한 지점에서 나온 광선이 이미지 평면에 완벽하게 수렴하지 않을 때, 그 광선은 단일 지점 대신 작은 원을 형성합니다.
    • 이를 착란원(Circle of Confusion, CoC)이라고 합니다.
  • 착란원의 크기는 최종 이미지에서 물체의 선명도를 직접적으로 결정합니다.
    • 착란원이 작을수록 이미지가 더 선명하고 초점이 잘 맞습니다.

    coc

  • 렌즈를 조정함으로써 사진가는 다양한 거리에 있는 물체에 대한 착란원의 크기를 제어하여 초점을 맞출 수 있습니다.

초점과 초점 거리 (Focal Point and Focal Length)

  • 초점(Focal Point)과 초점면(Focal Plane)의 개념은 광선이 사실상 평행한 무한 거리의 물체에서 발생하는 광선에 고유합니다.
    • 이 시나리오에서 모든 평행 광선은 초점면의 단일 지점인 초점(Focal Point)으로 수렴합니다.
  • 초점 거리(Focal Length)는 렌즈의 광학 중심과 주 초점 사이의 거리입니다.
    • 실제 카메라의 경우, 피사체가 무한 거리에 있으면 이미지 평면은 초점면과 같은 위치에 있습니다.
      • 따라서 초점 거리는 렌즈의 광학 중심에서 이미지 센서까지의 거리로 간주될 수 있습니다.
  • 렌즈는 단일 초점 거리(고정 초점 거리)를 가진 단 렌즈(prime) 또는 가변 초점 거리를 가진 줌 렌즈(zoom)로 분류됩니다.
    • 줌 렌즈는 내부 요소를 움직여 초점 거리를 변경하며, 이는 시야를 변경합니다.

    focal_length

시야와 줌 (Field of View and Zooming)

  • 시야(Field of View, FOV)는 주어진 순간에 볼 수 있는 관찰 가능한 세계의 범위입니다.
    • 사진 및 컴퓨터 그래픽스에서 이는 카메라가 장면을 얼마나 많이 포착할 수 있는지를 결정하는 각도이며, 본질적으로 원근감과 줌 수준을 제어합니다.
  • 실제 세계에서 카메라의 시야는 초점 거리와 본질적으로 연결되어 있습니다.
    • 고정된 초점 거리(예: 50mm 렌즈)를 가진 특정 렌즈는 특정하고 협상 불가능한 시야를 갖습니다.
      • 초점 거리가 길수록(망원 렌즈) 시야가 좁아져 장면을 확대하고 “줌 인” 효과를 생성합니다.
      • 반대로, 초점 거리가 짧을수록(광각 렌즈) 시야가 넓어지고 장면을 더 많이 포착하여 “줌 아웃” 효과를 생성합니다.
  • 실제 카메라와 달리,
    • 컴퓨터 그래픽스 엔진은 물리적으로 정확하지는 않지만 더 큰 창의적 제어를 위해 초점 거리와 독립적으로 시야를 설정할 수 있도록 허용하는 경우가 많습니다.

    fov

조리개 (Aperture)

  • 광학 시스템에서 조리개(aperture)는 렌즈로 들어오는 빛의 양을 제어하는 구멍입니다.
  • 조리개가 클수록 더 넓은 범위의 각도에서 빛이 들어올 수 있으므로, 렌즈가 이 광선들을 단일 초점에 수렴시키기가 더 어려워집니다.
    • 이로 인해 정확한 초점 거리에 있는 물체는 선명한 이미지를 형성하는 반면, 다른 거리에 있는 물체는 더 큰 착란원(CoC)으로 인해 점진적으로 더 흐릿하게 보입니다.

  • 조리개의 크기는 일반적으로 f-수(f-number, N) 또는 f-스톱으로 표시되며, 이는 렌즈의 초점 거리($f$)와 유효 조리개 직경($D$)의 비율로 계산됩니다.

    \[N={f\over D}\]

  • 고정 초점 거리 렌즈(즉, 줌이 없는 렌즈)의 경우 f-수는 조리개 직경에 반비례합니다.

    aperture    

  • 조리개는 f-수를 통해 이 평면 밖에 있는 물체의 흐림 정도를 결정합니다.
    • f-수가 증가하면 조리개 직경이 감소합니다.
      • 이는 렌즈로 들어오는 광선 각도를 줄여 착란원을 축소시킵니다.
      • 결과적으로 초점 거리 이외의 거리에 있는 물체는 덜 흐릿하게 보입니다.
    • 반대로, f-수가 감소하면 조리개 직경이 증가합니다.
      • 이는 입사광의 각도를 넓혀 착란원을 확장하고 초점 거리 밖에 있는 물체가 더 흐릿하게 보이게 합니다.

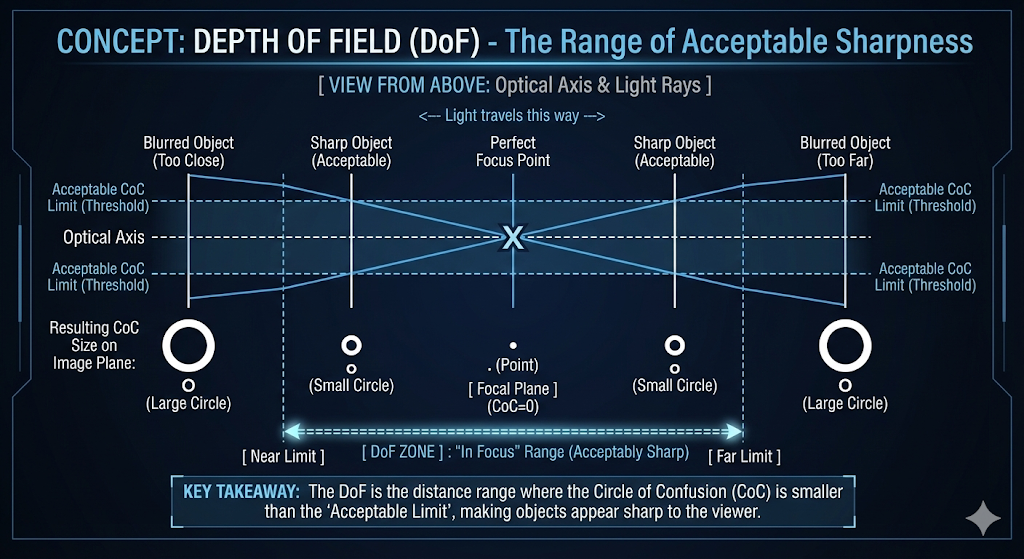
피사계 심도 (Depth of Field)

  • 피사계 심도(depth of field, DoF)는 이미지에서 허용 가능한 정도로 선명하게 보이는 장면 내 거리의 범위입니다.
    • 물체가 “초점이 맞았다”고 간주되는 것은 이미지 평면에 반사된 광선으로 형성된 착란원(CoC)이 시청자가 단일 지점으로 인식할 수 있을 만큼 충분히 작을 때입니다.
  • 착란원의 크기는 물체가 초점면으로부터 얼마나 떨어져 있는지에 따라 달라집니다.
    • 피사계 심도가 넓다는 것은 더 넓은 범위의 거리가 초점이 맞은 것처럼 보인다는 의미입니다.
    • 이는 초점면에서 상당히 멀리 떨어진 물체라도 DoF 경계 내에 남아 있는 한 허용 가능한 정도로 선명하게 보일 수 있음을 시사합니다.

    dof

초점 맞추기 (Focusing)

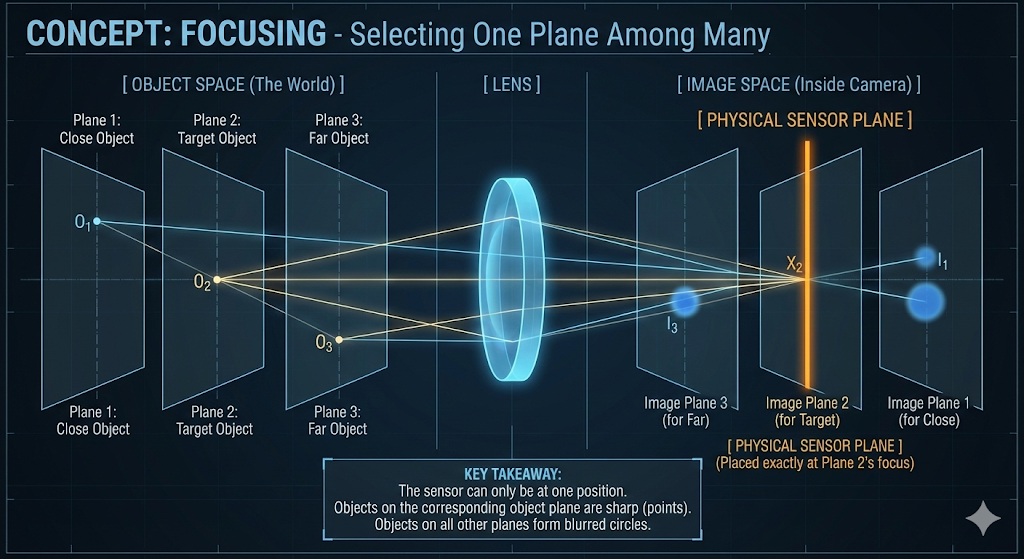
  • 카메라가 장면을 포착할 때, 모든 물체는 카메라로부터 특정 깊이 또는 거리에 존재합니다.
  • 세계가 카메라의 뷰 방향에 수직인 수많은 평행한 물체 평면(object planes)으로 구성되어 있다고 생각해 보십시오.
    • 이상적으로는 단일 물체 평면의 지점에서 발생하는 광선이 카메라 내의 단일 해당 이미지 평면(image plane)으로 수렴될 것입니다.
    • 이는 각 물체 평면이 광선이 완벽하게 초점이 맞춰지는 자체의 고유한 이미지 평면을 가지고 있음을 의미합니다.
  • 그러나 카메라의 센서는 주어진 순간에 단 하나의 고정된 이미지 평면만 차지할 수 있습니다.
    • 이 평면이 렌더링을 위해 선택되면, 다른 모든 평면의 물체에서 오는 광선은 선명하게 초점이 맞지 않을 것입니다.
    • 이 광선들은 단일 지점으로 수렴하는 대신, 선택된 이미지 평면과 착란원(CoC)이라고 알려진 흐릿한 원반으로 교차할 것입니다.
    • 이 원의 크기가 해당 특정 지점의 흐림 정도를 결정합니다.

    focusing

이미지 평면을 선택하는 방법 (How to Choose the Image Plane)

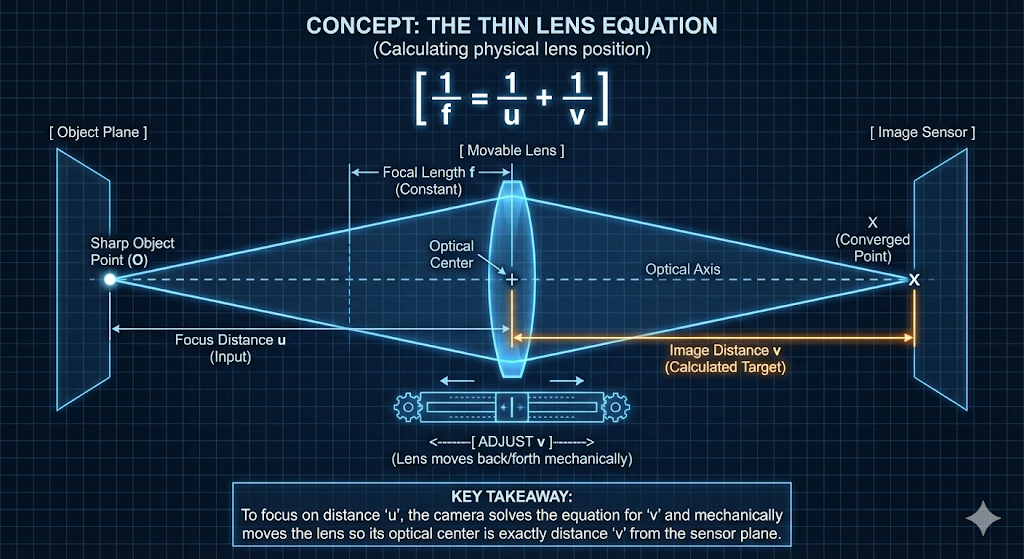
  • 카메라는 얇은 렌즈 방정식(Thin Lens Equation)으로 설명되는 과정을 통해 내부 광학 장치를 조정하여 렌더링할 적절한 이미지 평면을 결정합니다:     \({1\over f} = {1\over u} + {1\over v}\)    
    • 여기서
      • $f$는 렌즈의 초점 거리입니다.
      • $u$는 초점 거리(focus distance)로, 완벽하게 초점을 맞추려는 물체 평면에서 렌즈까지의 거리입니다.
      • $v$는 이미지 거리(image distance)로, 렌즈의 광학 중심에서 이미지 센서 또는 이미지 평면까지의 거리입니다.
        • 이는 초점을 달성하기 위해 물리적으로 조정되는 변수입니다.
  • 얇은 렌즈 방정식은 주어진 초점 거리($f$)에 대해 이미지 거리($v$)가 초점 거리($u$)에 의해 고유하게 결정됨을 보여줍니다.
    • 따라서 특정 거리에 있는 물체에 초점을 맞추는 것은 이미지 센서에 대한 렌즈 어셈블리를 물리적으로 이동함으로써 달성됩니다.
    • 이 광학 중심의 물리적 움직임은 원하는 물체 평면에서 오는 광선이 카메라 센서에 정확하게 수렴되도록 보장하여 해당 물체에 선명하게 초점을 맞춥니다.

    choosing_image_plane

시각 효과 구현 (Implementing Visual Effects)

디포커스 블러 (피사계 심도) (Defocus Blur (Depth of Field))

  • 디포커스 블러(Defocus blur)는 일반적으로 피사계 심도(DoF)로 알려져 있으며, 물체가 카메라의 초점 범위 내에 있지 않을 때 발생하여 착란원(CoC)이 눈에 띄게 커지는 현상입니다.
  • 실시간 렌더링에서 이 물리적 프로세스를 시뮬레이션하는 것은 계산 비용이 많이 듭니다.
    • 따라서 일반적인 대안은 G-버퍼(G-Buffer)를 사용하는 후처리 기법입니다.
  • G-버퍼는 깊이, 위치 및 표면 법선을 포함하여 픽셀당 데이터를 저장합니다.
    • 그런 다음 후처리 셰이더는 이 깊이 정보를 사용하여 픽셀이 카메라의 초점면에서 떨어진 거리를 기반으로 각 픽셀에 대한 블러 반경을 계산합니다.
      • 픽셀의 깊이가 DoF 경계 내에 있으면,
        • 해당 착란원(CoC) 반경은 0으로 설정됩니다(흐림 없음).
      • 픽셀의 깊이가 경계 밖에 있으면,
        • 셰이더는 블러 반경을 계산합니다.
      • 이 반경은 픽셀의 깊이가 초점 내 경계에서 얼마나 멀리 떨어져 있는지에 따라 배율이 조정됩니다.
        • 픽셀이 초점면에서 멀어질수록 계산된 블러 반경이 더 커집니다.

  • DoF 내의 픽셀은 거의 또는 전혀 흐림이 적용되지 않는 반면, 그 밖의 픽셀은 초점면에서의 거리에 따라 흐려져 디포커스 효과를 시뮬레이션합니다.

    defocus_blur

모션 블러 (Motion Blur)

  • 모션 블러(Motion blur)는 짧은 노출 시간의 결과로 움직이는 물체의 번짐을 시뮬레이션하는 효과입니다.
    • 이는 디포커스 블러가 공간 영역에 걸쳐 샘플을 평균화하여 달성되는 것과 유사하게, 여러 프레임 또는 시간 단계에 걸쳐 픽셀의 색상을 평균화하여 구현됩니다.

  • 픽셀의 최종 색상은 시간의 다른 순간에서의 색상의 혼합이며, 움직임의 착시를 만듭니다.

    motion_blur

  • Click to see the code 
      Ray getRayToSample(int currentWidth, int currentHeight) const {
      auto offset = getSampleSquare();
      auto pixelSample = pixelCenterTopLeft
          + ((currentWidth + offset.getX()) * pixelDeltaWidth)
          + ((currentHeight + offset.getY()) * pixelDeltaHeight);

      auto rayOrigin = (defocusAngle <= 0) ? center : getDefocusRandomPoint();
      auto rayDirection = pixelSample - rayOrigin;
      auto rayTime = getRandomDouble();

      return Ray(rayOrigin, rayDirection, rayTime);
  }

기본 요소 교차: 장면 탐색의 비용 (Primitive Intersection: The Cost of Scene Traversal)

  • 카메라가 광선을 생성한 후, 가장 중요한 작업은 그 광선이 장면의 기하학적 기본 요소와 교차하는 위치와 여부를 결정하는 것입니다.
    • 구(sphere)나 삼각형과 같은 단순한 모양은 교차 테스트가 간단하지만, 사각형(quadrilateral)과 같은 복잡한 기본 요소는 다단계 해석 기하학을 요구합니다.
  • 사각형(quad) 교차는 견고한 기하학적 처리를 보장하기 위해 광선-평면 테스트와 후속 경계 검사를 결합하는 2단계 프로세스를 필요로 합니다.

사각형 정의 (Quad Definition)

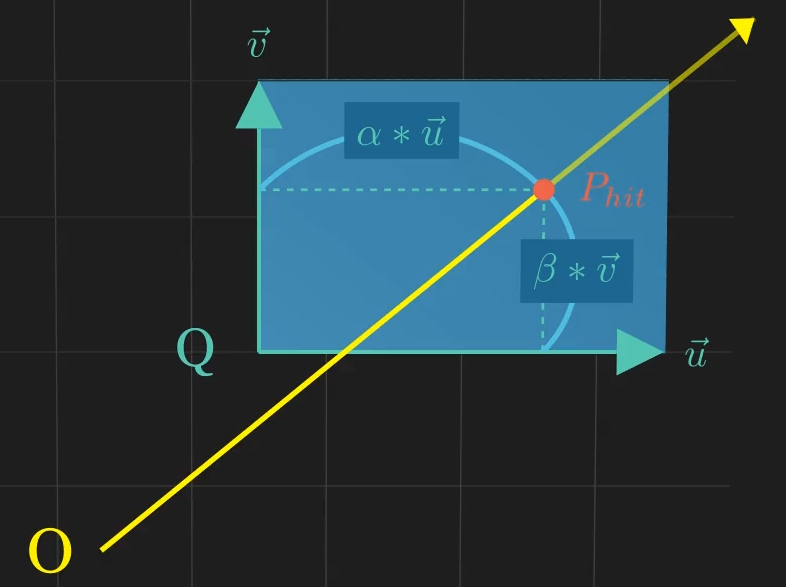
  • 사각형은 시작점 $\mathbf{Q}$와 두 방향 벡터 $\vec{u}$ 및 $\vec{v}$에 의해 매개변수적으로 정의됩니다. 무한 평면 상의 임의의 점 $\mathbf{P}(i, j)$는 다음과 같습니다:
\[\mathbf{P}(i, j) = \mathbf{Q} + i\vec{u} + j\vec{v}\]
  • 사각형 자체는 $\mathbf{0 \le i \le 1}$ 및 $\mathbf{0 \le j \le 1}$로 제한된 영역입니다.

2단계 교차 논리 (The Two-Step Intersection Logic)

  1. 광선-평면 교차 (시간 $t$): 광선 및 평면 방정식을 $t$에 대해 풀어 사각형을 포함하는 무한 평면 상의 교차점 $\mathbf{P_{hit}}$을 찾습니다.
\[\mathbf{t} = \frac{(\mathbf{Q} - \mathbf{O}) \cdot \mathbf{n}}{\mathbf{d} \cdot \mathbf{n}}\]
  1. 점 포함 검사 (매개변수 $\alpha, \beta$): 매개변수 $\alpha$와 $\beta$를 계산하고 이들이 0과 1 사이에 있는지 확인하여 교차점 $\mathbf{P_{hit}}$이 사각형의 정의된 경계 내에 있는지 확인합니다.
\[\mathbf{\alpha} = \frac{(\mathbf{P_{hit}} - \mathbf{Q}) \times \vec{v} \cdot \mathbf{n}}{(\vec{u} \times \vec{v}) \cdot \mathbf{n}}\] \[\mathbf{\beta} = \frac{\vec{u} \times (\mathbf{P_{hit}} - \mathbf{Q}) \cdot \mathbf{n}}{(\vec{u} \times \vec{v}) \cdot \mathbf{n}}\]

  • 성공 조건: 광선이 사각형을 맞추는 경우는 $\mathbf{t \ge 0}$ 및 $\mathbf{0 \le \alpha \le 1}$ 및 $\mathbf{0 \le \beta \le 1}$일 때입니다.

    intersection

안티앨리어싱 (Anti-Aliasing)

  • 앨리어싱은 컴퓨터 그래픽스에서 날카로운 모서리와 선이 들쭉날쭉하거나 “계단 모양(stair-stepped)“으로 보이는 일반적인 시각적 문제입니다.
  • 이는 연속적이고 부드러운 3D 장면이 화면의 이산적인 픽셀 격자에 투영되기 때문에 발생합니다.
    • 각 픽셀은 단일하고 단단한 색상만 표시할 수 있습니다. 이 문제의 핵심 원인은 점 샘플링(point sampling)이라는 프로세스입니다.

앨리어싱이 발생하는 이유 (Why Aliasing Occurs)

  • 레이 트레이싱에서 픽셀의 색상은 전통적으로 카메라에서 픽셀의 중심을 통과하여 장면으로 단일 광선을 발사하여 결정됩니다.
    • 광선이 맞춘 물체의 색상이 전체 픽셀에 사용됩니다.
  • 문제는 단일 픽셀이 단일 점이 아니라 장면의 작은 정사각형 영역을 나타낸다는 것입니다.
    • 예를 들어, 검은색 물체가 흰색 배경과 만나는 날카로운 모서리가 해당 픽셀 영역 내에 있으면, 중앙으로 발사된 단일 광선은 흰색 배경만 맞출 수 있습니다.
    • 모서리의 검은색 부분은 완전히 놓치게 됩니다.
  • 이 “전부 아니면 전무(all-or-nothing)” 접근 방식은 세부 정보 손실로 이어져 들쭉날쭉한 계단 모양을 유발합니다.
    • 픽셀의 색상은 단일 샘플로 결정되지만, 픽셀이 나타내는 영역은 장면에 여러 색상을 포함할 수 있습니다.

    aliasing

해결 방법 (How to Fix)

  • 해결책은 각 픽셀에 대해 단 하나의 광선 대신 여러 개의 광선을 발사하는 슈퍼샘플링(supersampling)을 사용하는 것입니다.
    • 핵심 아이디어는 픽셀 영역 내의 다른 위치를 샘플링한 다음, 결과 색상을 평균화하여 실제 색상을 더 정확하게 표현하는 것입니다.
    • 이 색상 혼합은 물체 간의 전환을 부드럽게 하여 들쭉날쭉한 모서리를 제거합니다.
  • 슈퍼샘플링 방법은 각 픽셀 내에서 여러 샘플 위치를 선택하는 방식이 다릅니다:
    • 격자 샘플링 (Grid Sampling)
      • 픽셀은 규칙적인 격자(예: 2x2, 4x4)로 나뉘며, 각 서브 격자 셀의 중앙으로 광선이 발사됩니다.
        • 4x4 격자의 경우,
          • 16개의 광선이 발사되고
          • 이들의 평균 색상 값이 해당 셀의 색상 값이 됩니다.
      • 이 방법은 간단하고 효과적이지만, 때로는 미세한 세부 사항을 놓치거나, 샘플링 격자가 장면의 반복 패턴과 정렬되면 자체적인 시각적 아티팩트를 생성할 수 있습니다.
    • 지터드 샘플링 (Jittered Sampling):
      • 이는 더 진보된 기술입니다.
        • 이 역시 픽셀을 격자로 나누지만, 각 셀의 중앙으로 광선을 발사하는 대신, 각 셀 내의 무작위로 선택된 지점으로 광선을 발사합니다.
      • 이 작은 무작위성은 샘플이 픽셀 영역 전체에 고르게 분포되도록 보장하면서도, 격자 샘플링의 구조화된 아티팩트를 방지하는 데 도움이 됩니다.
      • 지터드 샘플링은 눈에 띄는 아티팩트가 적은 더 자연스럽고 정확한 결과를 생성합니다.

      anti_aliasing

후처리 및 최종 디스플레이 (Post-Processing & Final Display)

  • 렌더링 파이프라인의 최종 단계에는 선형 공간에서 계산된 빛 강도 값을 포함하는 고동적 범위(HDR) 이미지 데이터를 처리하고, 이를 표준 디스플레이에 적합한 지각적으로 올바른 저동적 범위(LDR) 이미지로 변환하는 과정이 포함됩니다.

톤 매핑: 동적 범위 압축 (Tonemapping: Compressing the Dynamic Range)

  • 톤 매핑(Tonemapping)은 렌더링된 HDR 이미지의 넓은 범위의 휘도(밝기) 값을 표준 모니터가 표시할 수 있는 좁은 범위로 매핑하는 매우 중요한 프로세스입니다.
  • 문제: 물리 기반 렌더링은 빛을 정확하게 계산하며, 종종 표준 LDR 이미지 파일(예: 8비트 JPEG)의 $0$에서 $1$ 범위를 초과하는 매우 밝은 값(예: 직사광선)을 초래합니다.
    • 조정 없이 이 값을 표시하면 하이라이트가 클리핑되어 디테일 손실이 발생합니다.
  • 해결책: 톤 매핑 오퍼레이터는 비선형 곡선을 적용하여 이미지의 밝은 부분을 압축하는 동시에 중간 톤과 그림자의 디테일을 보존합니다.
  • 널리 사용되는 두 가지 오퍼레이터는 다음과 같습니다:
    • 라인하르트 오퍼레이터(Reinhard Operator): 사진 노출 과정을 모델링하는 간단하고 계산 비용이 저렴한 오퍼레이터입니다.
      • 하이라이트를 부드럽게 압축하지만 때로는 다소 평평하거나 색이 바랜(washed-out) 모양을 초래할 수 있습니다.
      \[L_{out} = \frac{L_{in}}{1 + L_{in}}\]
      • 여기서 $L_{in}$은 선형 입력 휘도이고 $L_{out}$은 결과 LDR 휘도입니다.
    • ACES (Academy Color Encoding System): 특히 하이라이트에서 생생한 모양과 뛰어난 색상 채도 보존으로 알려진 보다 정교한 필름 룩(filmic) 톤 매핑 표준입니다.
      • 이는 시네마틱 색상 과학에서 파생된 복잡한 곡선을 사용하여 시각적으로 고품질 필름 스톡과 유사한 결과를 생성합니다.

    tonemapping

색상 변환 및 룩업 테이블 (LUTs) (Color Transformation and Look-Up Tables (LUTs))

  • 톤 매핑 후, 이미지는 특정 예술적 스타일을 적용하거나 색상 불균형을 수정하기 위해 색상 변환(Color Transformation)을 거칩니다. 이는 종종 룩업 테이블(Look-Up Table, LUT)을 사용하여 수행됩니다.
    • 목적: LUT는 픽셀의 원래 RGB 값을 기반으로 픽셀의 색상을 빠르게 수정하는 데 사용되는 미리 계산된 데이터 세트입니다.
    • 구현: LUT는 종종 $3\text{D}$ 텍스처 큐브로 구현됩니다.
      • 픽셀의 원래 RGB 색상은 LUT 큐브를 샘플링하는 좌표 $(r, g, b)$ 역할을 합니다.
      • 큐브의 해당 좌표에 저장된 값은 새롭고 변환된 RGB 색상입니다.
    • 효율성: LUT를 통해 복잡한 색상 보정 작업(예: 대비 또는 화이트 밸런스 변경)을 적용하는 것은 픽셀당 단일 텍스처 조회 작업만 포함하므로, 모든 픽셀에 대해 긴 수학적 함수를 실행하는 것보다 훨씬 빠릅니다.

    lut

감마 보정 (디스플레이 출력) (Gamma Correction (Display Output))

  • 게시물 1에서 확립된 바와 같이, 최종 톤 매핑된 LDR 이미지는 모니터로 보내기 전에 선형 공간(Linear Space)에서 감마 공간(Gamma Space, sRGB)으로 다시 변환되어야 합니다.
\[\mathbf{C}_{\text{gamma}} = (\mathbf{C}_{\text{linear}})^{1/\gamma}\]
  • 이 최종 변환은 이미지가 지각적으로 균형을 이루도록 보장하며, 디스플레이 하드웨어의 비선형 반응을 설명하여 이미지가 사람의 눈에 올바르게 보이도록 합니다.

Top

Leave a comment

You may also enjoy