Computer Graphics: Optimization
최적화 (Optimization)
- 고성능 게임 엔진에서 최적화는 단순히 코드 정리 이상의 의미를 갖습니다.
- 이는 하드웨어 아키텍처, 수학적 효율성, 그리고 공간 조직화에 대한 깊은 이해를 요구합니다.
- 이 섹션에서는 렌더링 및 물리 계산을 가속화하기 위해 사용되는 주요 전략을 간략하게 설명합니다.
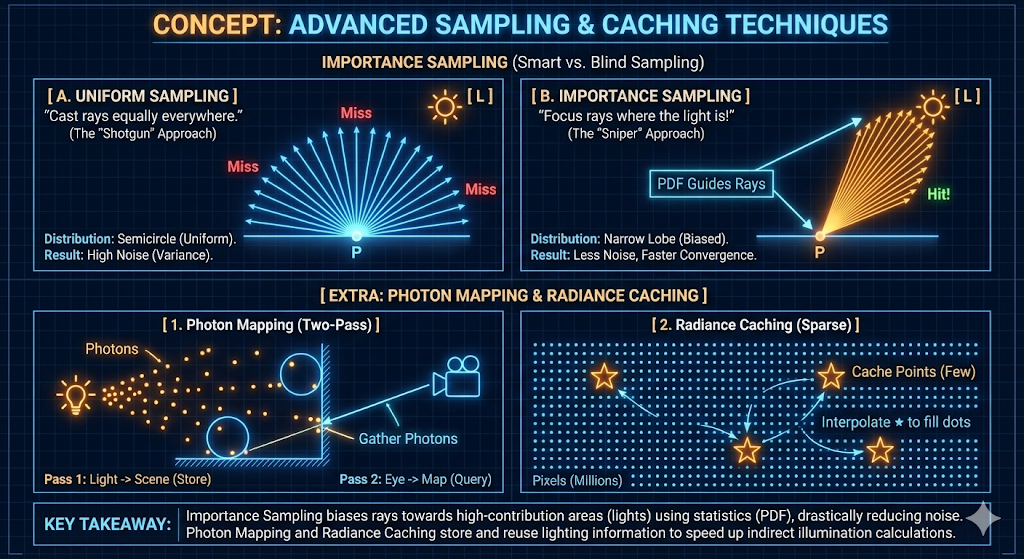
고급 샘플링 및 캐싱 기술 (Advanced Sampling and Caching Techniques)
레이 트레이싱의 확률적 특성을 해결하기 위해, 샘플 수를 과도하게 늘리지 않고도 노이즈를 줄이고 수렴 속도를 높이는 여러 기술이 사용됩니다.
- 중요도 샘플링 (Importance Sampling): 모든 방향으로 광선을 균일하게 발사하는 대신, 광선 방향을 최종 이미지에 가장 크게 기여하는 경로, 즉 광원 쪽이나 정반사(specular reflection) 벡터를 따라 편향되게 설정합니다. 이 통계적 편향은 고기여 영역을 샘플링할 확률을 대폭 증가시켜 더 빠른 수렴과 감소된 분산(노이즈)을 가져옵니다.
- 포톤 매핑 (Photon Mapping): 이는 2단계 전역 조명 알고리즘입니다. 첫 번째 단계(순방향 추적)는 광원에서 장면으로 “포톤“을 방출하고, 표면과 상호 작용하는 포톤을 공간 맵에 저장합니다. 두 번째 단계(카메라에서 역방향 추적)는 이 포톤 맵을 쿼리하여 간접 조명을 효율적으로 근사화합니다.
-
방사량 캐싱 (Radiance Caching): 확산 조명은 표면 전체에서 느리게 변화하기 때문에, 방사량(radiance) 값이 드문드문한 위치에서 계산되어 캐시에 저장됩니다. 후속 광선은 값비싼 전체 스펙트럼 평가를 수행하는 대신, 이 캐시된 값을 보간하여 간접 조명의 저주파 특성을 활용합니다.
저수준 CPU 최적화 (Low-Level CPU Optimization)
현대 CPU 아키텍처는 명령어 파이프라이닝에 크게 의존합니다. 효율적인 코드는 예측 불가능한 실행 경로로 인해 발생하는 파이프라인 정지(stall)를 최소화해야 합니다.
분기 예측 및 분기 없는 프로그래밍 (Branch Prediction and Branchless Programming)
- 문제 (분기 예측 실패): CPU는 조건문(
if/else)의 결과를 예측하고 명령어들을 파이프라인에 미리 로드하기 위해 분기 예측을 사용합니다. 예측이 실패하면 (“miss”), 파이프라인을 비워야 하며, 이는 정지(Stall)라고 알려진 상당한 지연을 유발합니다. 광선 교차와 같은 고빈도 루프에서 이 페널티는 심각합니다. -
해결책 (분기 없는 코드, Branchless Code): 조건부 점프는 가능한 한 산술 또는 비트 연산으로 대체되어야 합니다. 예를 들어,
min()/max()함수나 조건부 이동(conditional moves)을 활용하면 CPU가 파이프라인 플러시 위험 없이 명령어를 선형적으로 실행할 수 있습니다.
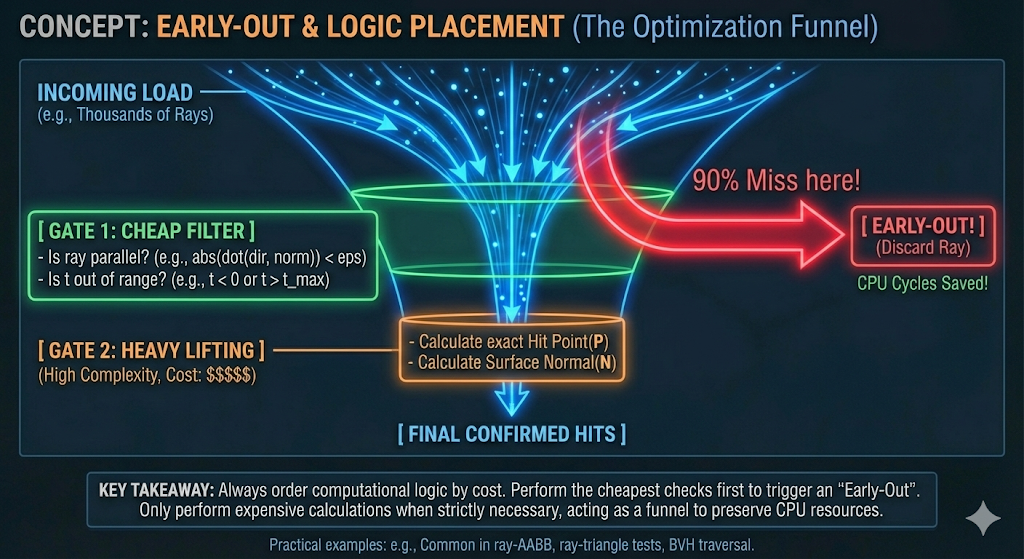
조기 종료 및 로직 배치 (Early-Out and Logic Placement)
- 복잡성 관리: 계산 로직은 비용 순서대로 배열되어야 합니다. 가장 비용이 저렴한 검사(가장 낮은 계산 복잡도)를 먼저 수행하여 조기 종료(Early-Out)를 트리거해야 합니다.
-
적용 (광선-AABB): 정확한 교차점을 계산하기 전에, 광선이 평판과 평행한지($D_x \approx 0$) 또는 진입 시간이 퇴장 시간을 초과하는지($t_{start} > t_{end}$)와 같은 간단한 검사를 실행합니다. 이는 정확한 충돌에 필요한 값비싼 대수 연산이 엄격하게 필요할 때만 수행되도록 보장하여 CPU 사이클을 절약합니다.
인스턴싱 및 공간 변환 (Instancing and Spatial Transformations)
인스턴싱은 단일 메쉬를 재사용하면서 고유한 변환(SRT)을 적용하여 전역 공간(Global Space)에 객체를 배치하는 근본적인 최적화입니다. 변환은 열 벡터 규칙(column-vector convention)을 사용하여 계산되며, 연산 순서는 오른쪽에서 왼쪽으로 적용됩니다: 축척 $\rightarrow$ 회전 $\rightarrow$ 이동.
변환의 기하학: 공간 변환 (The Geometry of Transformation: Space Transformation)
공간 변환(Space Transformation)의 개념은 인스턴싱 및 효율적인 장면 관리의 기본입니다. 이를 통해 자체 로컬 공간(Local Space)에서 정의된 객체가 전역 장면 좌표(Global Space) 내에 올바르게 배치, 방향 설정 및 축척이 적용될 수 있습니다.
동차 좌표를 통한 행렬 표현 (Matrix Representation via Homogeneous Coordinates)
- 변환은 실제로 동차 좌표($\mathbf{x, y, z, w}$)와 결합된 $4 \times 4$ 행렬을 사용하여 실행됩니다.
- ‘w’ 좌표:
- $w=1$: 벡터는 위치를 나타내며 이동의 영향을 받습니다.
- $w=0$: 벡터는 방향을 나타내며 이동의 영향을 받지 않습니다.
- ‘w’ 좌표:
- 변환 행렬($\mathbf{M}$)은 그 열이 세 개의 기본 축과 새 공간의 원점을 정의하는 간결한 표현입니다:
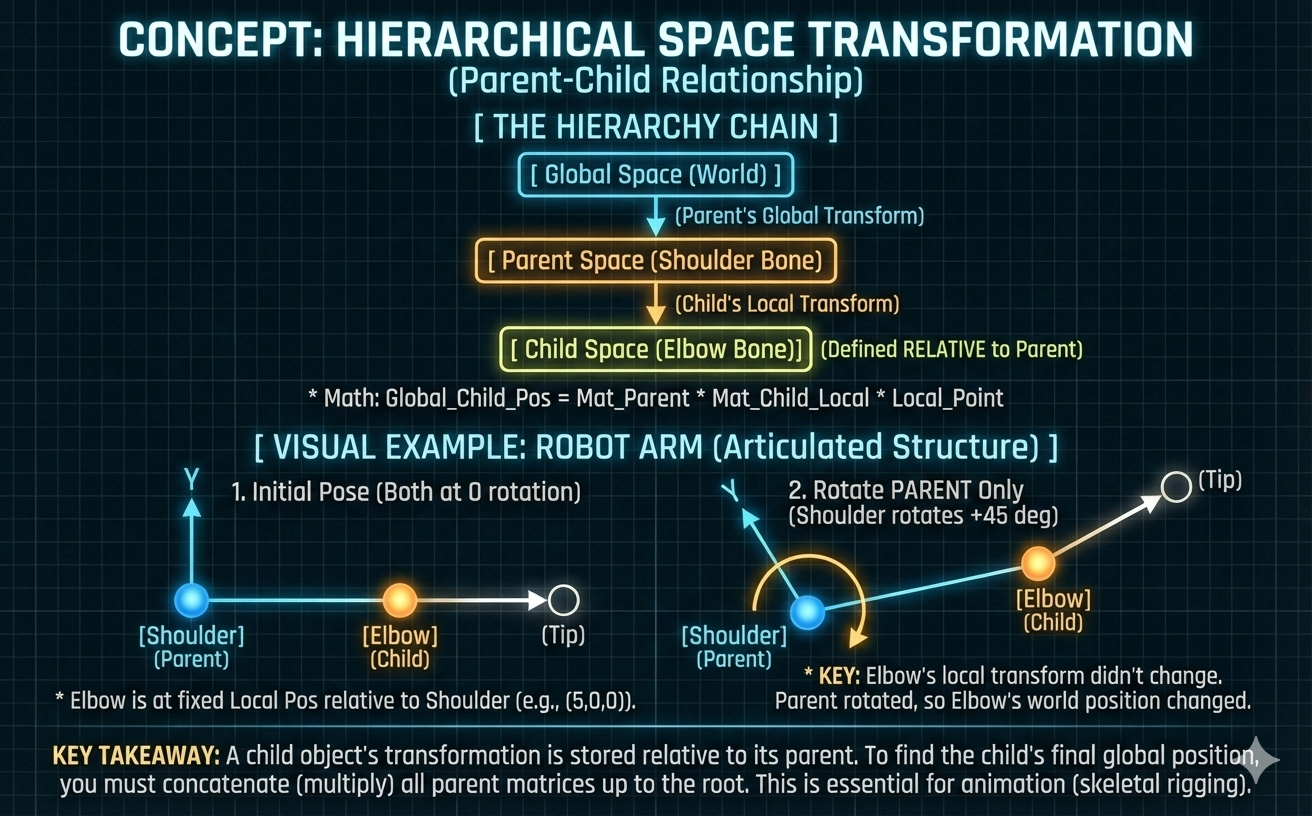
계층적 공간 변환 (Hierarchical Space Transformation)
- 복잡한 장면과 모델은 효율적인 관리를 위해 연결된 공간의 계층 구조(예: 전역 $\rightarrow$ 부모 $\rightarrow$ 자식)를 사용합니다.
- 핵심 원리: 객체의 로컬 변환은 부모의 좌표계를 기준으로 적용됩니다. 전역 위치는 로컬 공간에서 루트 공간까지 모든 조상 공간의 변환 행렬을 연속으로 연결하여(순서대로 곱하여) 찾습니다.
- 애니메이션에서의 적용: 이 계층적 원리는 스키닝 및 리깅에 매우 중요합니다. 애니메이션 데이터는 각 뼈(Bone)에 대한 로컬 변환만 부모를 기준으로 저장하여 높은 효율성을 보장합니다. 최종 월드 행렬은 이 로컬 행렬을 뼈 체인을 따라 재귀적으로 곱하여 계산되며, 이는 GPU를 사용하여 고도로 최적화됩니다.
변환 파이프라인 (SRT)
- 최종 모델 행렬($M_{model}$)은 다음과 같이 곱하여 구성됩니다:
-
변환 시퀀스는 점 벡터 $\mathbf{v}$에 $\mathbf{v}’ = M_{model} \mathbf{v}$로 적용됩니다.
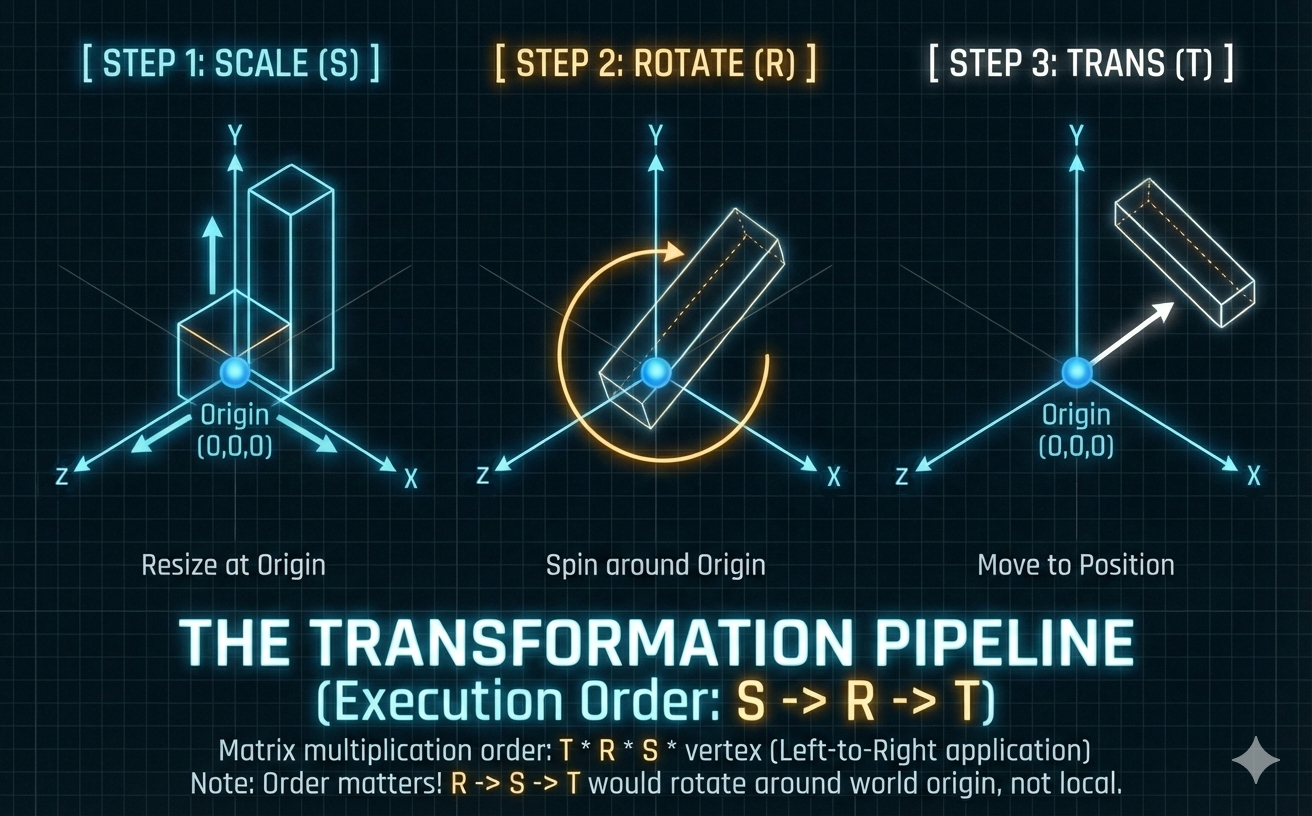
축척 ($\mathbf{S}$)
- 이것은 적용되는 첫 번째 연산입니다. 이는 대각 행렬(여기서는 3D 동차 좌표용)을 사용하여 객체를 로컬 축을 따라 늘리거나 줄입니다.
- 반전(Mirroring)에 대한 참고: 음의 축척(예: X축에서 -1)을 적용하면 객체가 YZ 평면을 가로질러 반전됩니다. 이는 정점의 감기 순서(winding order)를 반전시키므로, 올바른 조명 계산을 유지하기 위해 표면 법선을 뒤집어야 할 수 있습니다.
회전 ($\mathbf{R}$)
- 이것은 적용되는 두 번째 연산입니다. 이는 객체의 방향을 정의합니다. Z축을 중심으로 $\theta$만큼 회전하는 경우:
- 역회전($-\theta$)의 경우, 삼각 함수의 속성($\sin(-\theta) = -\sin\theta$, $\cos(-\theta) = \cos\theta$)이 사용되어 회전 행렬의 전치(transpose)가 됩니다(회전 행렬은 직교 행렬이므로).
이동 ($\mathbf{T}$)
- 이것은 적용되는 최종 연산입니다. 이는 로컬 공간 원점 $(0,0,0)$을 새 전역 위치 $(T_x, T_y, T_z)$로 이동시킵니다.
회전 행렬의 유도 (Derivation of the Rotation Matrix)
- Z축을 중심으로 각도 $\theta$만큼 회전하는 $2\times2$ 회전 행렬은 기본 벡터 $\hat{\mathbf{x}} = (1, 0)$와 $\hat{\mathbf{y}} = (0, 1)$가 어떻게 변환되는지를 관찰하여 유도됩니다.
X축 기본 벡터 변환
-
X축의 단위 벡터 $P_x = (1, 0)$는 $\theta$만큼 회전할 때 새 위치 $P_{x’}$로 이동합니다:
\[P_{x'} = (\cos\theta, \sin\theta)\] -
이 벡터는 회전 행렬의 첫 번째 열을 형성합니다.
Y축 기본 벡터 변환
-
Y축의 단위 벡터 $P_y = (0, 1)$는 $\theta$만큼 회전할 때 다음으로 이동합니다:
\[P_{y'} = (-\sin\theta, \cos\theta)\] -
이 벡터는 회전 행렬의 두 번째 열을 형성합니다.
최종 회전 행렬
- 이 두 개의 새로운 기본 벡터를 열로 적용하면 임의의 벡터 $(x, y)$를 회전할 수 있습니다:
- 결과 좌표는 다음과 같습니다:
역변환 및 성능 (Inverse Transformation and Performance)
- 모델 행렬의 역행렬은 전역 공간의 점을 로컬 공간으로 다시 변환하는 데 필요합니다:
- 전체 역행렬을 계산하는 것은 계산 비용이 많이 듭니다.
- 그러나 회전 행렬 ($\mathbf{R}$)은 직교 행렬(Orthogonal Matrix)입니다 ($\mathbf{R}^{-1} = \mathbf{R}^{T}$).
- 이를 통해 역회전 구성 요소를 간단한 전치 연산으로 계산할 수 있으므로, 광선이나 벡터를 객체의 로컬 공간으로 변환할 때 상당한 성능 향상을 제공합니다.
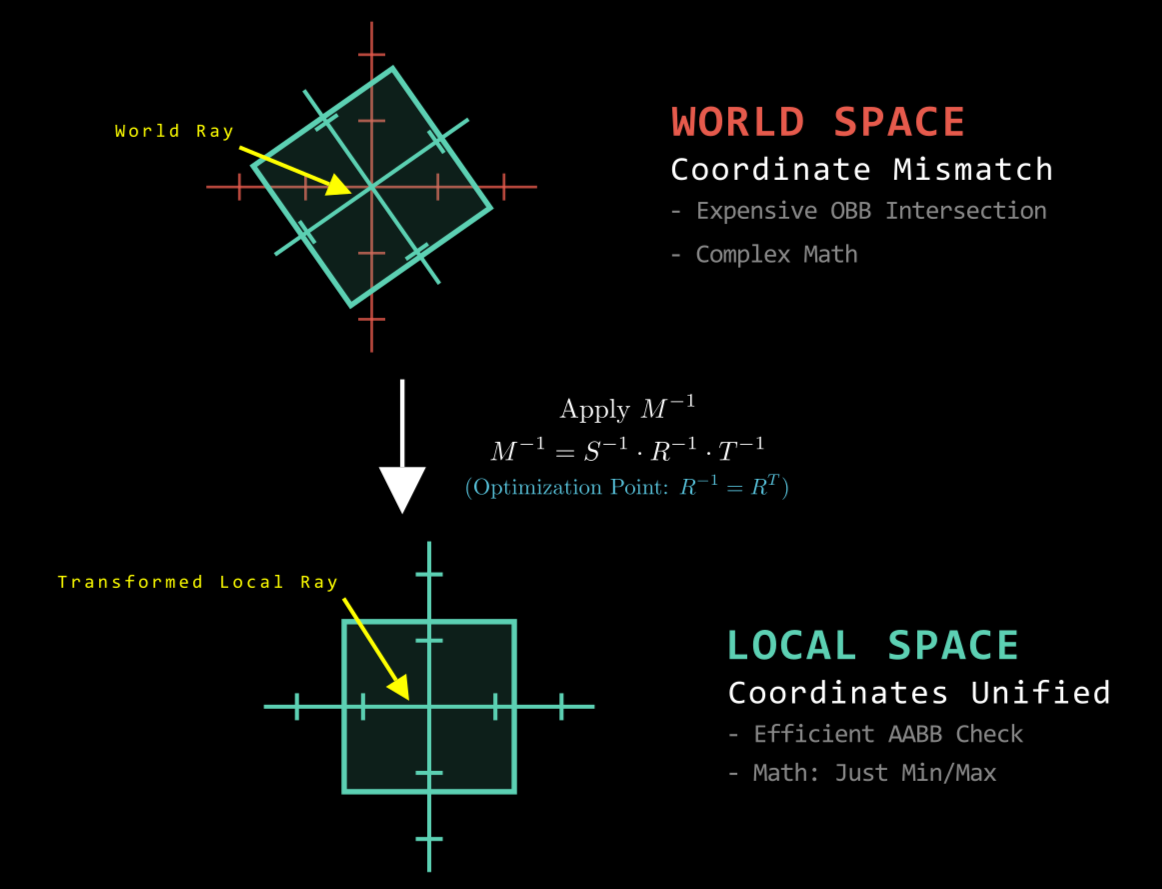
최적화: 역 광선 방법 (Optimization: The Inverse Ray Method)
-
회전된 인스턴스에 대한 충돌 감지의 순진한 접근 방식은 AABB를 회전시키는 것인데, 이는 경계를 느슨하게 하고 효율성을 떨어뜨립니다. 더 우수한 접근 방식은 광선을 객체의 로컬 공간으로 변환하는 것입니다.
- 개념: 월드 공간에서 “광선 대 회전된 상자”를 검사하는 대신, 엔진은 로컬 공간에서 “역변환된 광선 대 축 정렬 상자”를 검사합니다.
-
구현: 광선 $R(t) = Q + t\vec{d}$는 역 모델 행렬($S^{-1} \cdot R^{-1} \cdot T^{-1}$)을 사용하여 변환됩니다. 로컬 공간에서 객체는 항상 축 정렬되어 있으므로, 복잡한 OBB(Oriented Bounding Box) 테스트 대신 고도로 최적화된 AABB 교차 알고리즘을 사용할 수 있습니다.
추가 참고: AI/머신러닝과의 연결 (Extended Note: The Connection to AI/Machine Learning)
- 공간 변환의 근본 원리는 AI/머신러닝의 핵심 작업으로 직접 확장됩니다.
- AI 계층은 주로 행렬 곱셈으로 구성되며, 이는 입력 데이터에 공간 변환의 연속적인 시리즈를 적용하는 것으로 볼 수 있습니다.
- 머신러닝은 이 변환 행렬 내의 요소(가중치)를 조정하여 입력 데이터 공간을 최종적으로 원하는 출력 공간(예측)으로 매핑하는 반복적인 프로세스입니다.
경계 볼륨 계층 구조 (BVH) 종합 검토 (Bounding Volume Hierarchy (BVH) Comprehensive Review)
경계 볼륨 계층 구조(Bounding Volume Hierarchy, BVH)는 실시간 레이 트레이싱과 같이 계산 집약적인 작업을 가능하게 하는 데 사용되는 핵심 공간 분할 데이터 구조입니다. BVH의 주요 목표는 광선-기본 요소 교차 테스트의 수를 극적으로 줄여서 계산 복잡도를 $O(M)$ (선형 검색)에서 $O(\log M)$ (로그 검색)으로 낮추는 것입니다.
핵심 개념 및 작동 원리 (Core Concept and Operating Principle)
- BVH의 근본적인 아이디어는 최적화 마인드셋에서 비롯됩니다: 수천 개의 복잡한 기하학적 테스트를 최소한의 빠른 볼륨 검사로 대체하는 것입니다.
기본 구조: 빠른 거부 (Basic Structure: Rapid Rejection)
- 기본 요소 포장: 모든 단일 삼각형이나 객체($M$ 기본 요소)에 대해 광선 테스트를 수행하는 대신, 객체 그룹을 경계 볼륨(bounding volume)(일반적으로 축 정렬 경계 상자, AABB)이라는 간단한 컨테이너로 포장합니다.
- 조기 거부: 광선이 AABB와 교차하는지 확인하는 데는 몇 가지 간단한 산술 비교만 필요합니다. 광선이 AABB를 놓치면, 그 안에 포함된 모든 복잡한 기하학을 놓치는 것이 보장됩니다. 이를 통해 단 한 번의 빠른 테스트로 대규모 기하학 그룹을 즉시 조기 종료(Early-Out)할 수 있습니다.
계층적 구조 및 2단계 탐색 (Hierarchical Structure and Two-Stage Traversal)
단일 경계 상자는 복잡한 장면을 처리할 수 없으므로, 이 볼륨들은 일반적으로 이진 트리 형태의 계층적 구조로 조직됩니다.
- 고수준 탐색: 광선은 루트 노드에서 시작하여 BVH를 탐색합니다. 각 노드의 경계 상자가 먼저 검사되며, 놓치면 전체 서브트리가 안전하게 폐기됩니다.
-
저수준 검사: 광선이 리프 노드(일반적으로 1~4개의 적은 수의 기본 요소를 포함)에 도달할 때만 실제 기하학에 대한 비용이 많이 드는 교차 테스트가 수행됩니다.
BVH 구성 및 최적화 (BVH Construction and Optimization)
- BVH의 성능 이득은 구조가 구축되는 방식에 크게 좌우됩니다.
구성 알고리즘 및 SAH (Construction Algorithm and SAH)
- 분할 방법: 일반적인 고품질 구성 방법은 하향식 분할(top-down partitioning)입니다. 이는 모든 객체를 포괄하는 단일 볼륨으로 시작하여 이를 더 작은 볼륨으로 재귀적으로 나눕니다.
- 분할 기준: 효율적인 탐색을 위해 객체는 현재 경계 상자의 가장 긴 축을 따라 정렬됩니다. 그런 다음 객체 수의 절반과 같은 기준으로 분할이 수행됩니다.
- 정렬 이유: 정렬은 효율적인 공간 관리를 허용하며, 가장 긴 축을 따라 분할하면 결과 자식 노드의 표면적이 최소화됩니다.
- 표면적 및 최적화: 광선이 볼륨을 맞출 확률은 해당 볼륨의 표면적에 비례합니다. 표면적을 최소화하면 불필요한 교차 테스트 가능성이 줄어들어 최적화가 가속화됩니다.
- 표면적 휴리스틱 (Surface Area Heuristic, SAH): 가장 효과적인 분할은 자식 볼륨의 총 표면적의 합을 최소화하여 선택됩니다. 이는 평균 광선 탐색 비용을 최소화하기 위한 업계 표준 방법입니다.
동적 장면 최적화: 시간적 일관성 (Dynamic Scene Optimization: Temporal Coherence)
장면의 객체가 움직이는 동적 환경에서는 매 프레임마다 BVH를 완전히 재구축하는 비용을 완화해야 합니다.
- 시간적 일관성 활용: 이 기술은 연속적인 프레임 사이의 객체 움직임이 일반적으로 작다는 사실을 활용합니다.
- 구현: 이전 프레임의 BVH는 재사용되거나 빠르게 업데이트/재구성됩니다. 이는 처음부터 다시 구축하는 것보다 훨씬 빠르며, 전반적인 프레임 속도를 향상시키는 “프레임 수준 최적화“의 핵심 마인드셋입니다.
구현 심층 분석: AABB 교차 테스트 (평판 방법) (Deep Dive into Implementation: AABB Intersection Test (Slab Method))
- AABB 교차 테스트는 BVH 탐색의 핵심이며, 평판 방법(Slab method)이 고성능을 위해 분기 없는 코드 구현과 함께 사용됩니다.
평판 방법 및 $t_{enter}, t_{exit}$ 계산
- 평판 정의: AABB는 세 쌍의 평행한 평면(평판)의 교차로 간주됩니다.
-
시간 계산: 각 축($x, y, z$)에 대해 광선이 해당 평판에 진입($t_{min}$)하고 퇴장($t_{max}$)하는 매개변수 시간 $t$는 광선 방정식에서 계산됩니다:
\[t_{slab} = \frac{p_{plane} - Q_{origin}}{d_{axis}}\] - 분기 없는 코드: $t$ 값은 광선의 방향과 관련되므로, $\min() / \max()$ 함수가 $t_{min}$과 $t_{max}$를 결정하는 데 사용됩니다. 이는 조건문(if)을 제거하고 CPU의 분기 예측 실패로 인한 성능 저하(Stall)를 방지하는 핵심 최적화입니다.
-
최종 교차 검사: 세 축 모두에 대한 시간 간격의 교차점을 찾습니다:
\[t_{enter} = \max(t_{min\_x}, t_{min\_y}, t_{min\_z})\] \[t_{exit} = \min(t_{max\_x}, t_{max\_y}, t_{max\_z})\]교차는 $t_{enter} \le t_{exit}$일 때 유효합니다.
-
유효성 검사: 교차 시간은 $t_{enter} > 0$을 만족해야 합니다. 수치적 안정성을 위해 $t_{enter} > \mathbf{\epsilon}$ (엡실론)만 유효한 교차로 간주됩니다. (만약 $t_{enter} < 0$이면, AABB는 광선 원점 뒤에 있어 무효입니다.)
0 나누기 처리 및 역수 최적화 (Zero Division Handling and Reciprocal Optimization)
분모가 0인 상황(광선이 축에 평행함)을 처리하는 것은 교차 테스트의 견고성과 성능에 필수적입니다.
- 역수 사용: CPU에서는 곱셈이 나눗셈보다 빠르므로, 광선 방향 벡터의 역수($1/d_{axis}$)를 미리 계산하여 나눗셈을 곱셈으로 대체합니다.
- $d_{axis} = 0$ 처리: 만약 $d_{axis}$가 0이었다면, 그 역수는 미리 정의된 무한대 또는 매우 큰 값으로 처리됩니다. 무한대의 부호는 분자($p_{plane} - Q_{origin}$)의 부호에 의해 결정됩니다.
- 평행 및 놓침: 분모만 0이고 광선이 평판 밖에 있으면 교차는 발생하지 않으며, 즉시 조기 종료(Early-Out)가 수행됩니다.
- 평행 및 평면 위: 광선 원점이 정확히 평면 위에 있으면(형식 $0/0$), 수치적으로 NaN이 발생할 수 있습니다. 이는 AABB 경계를 $\epsilon$만큼 확장하는 등의 방법으로 처리되며, 안정성을 위해 일반적으로 교차하지 않는 것으로 간주됩니다.
BVH 대 옥트리: 공간 분할의 차이점 (BVH vs. Octree: Differences in Spatial Partitioning)
| 특징 | 경계 볼륨 계층 구조 (BVH) | 옥트리 / 쿼드트리 (Octree / Quadtree) |
|---|---|---|
| 핵심 개념 | 기본 요소 분할: 객체 중심 | 공간 분할: 공간 볼륨 중심 |
| 분할 방법 | 객체 수 및 SAH를 기반으로 하는 유연한 이진 분할 | 공간을 8개(3D)의 동일한 크기 볼륨으로 고정 분할 |
| 자식 노드 중첩 | 자식 경계 볼륨 간의 중첩이 허용됩니다. | 분할 간의 중첩이 없습니다(상호 배타적). |
| 물리/충돌 적용 | 자식 볼륨 중첩이 허용되어 객체 복제 문제를 방지합니다. 물리 엔진에서 선호됩니다. | 객체가 경계를 가로지를 경우 객체 복제 또는 특별 처리가 필요합니다. |
BVH 볼륨은 기하학적 분포에 따라 유연하게 형성되기 때문에, 복잡하고 균일하게 분포되지 않은 장면에서 옥트리의 고정 격자 분할보다 훨씬 효율적입니다.

부동 소수점 인코딩 (Floating-Point Encoding)
핵심 개념 (Core Concept)
- 부동 소수점 인코딩(Floating-Point Encoding)은 컴퓨터가 제한된 수의 비트 내에서 매우 작은 소수부터 매우 큰 크기까지 광범위한 실수 범위를 표현하는 데 사용하는 표준화된 방법입니다.
- 이 표현은 근본적으로 세 가지 필드로 구성됩니다:
- 부호 (Sign): 숫자가 양수인지 음수인지 결정합니다.
- 가수 (Mantissa, 또는 Significand): 숫자의 유효 자릿수 또는 정밀도를 저장합니다.
- 지수 (Exponent): 가수가 곱해지는 밑(일반적으로 2)의 거듭제곱을 저장합니다.

지수의 역할 (The Role of the Exponent)
- 부동 소수점 시스템은 지수를 사용하여 이진수에서 기수점(radix point)의 위치를 효과적으로 이동시킵니다.
- 이 이동은 표현할 수 있는 값의 범위를 극적으로 확장시킵니다.
- 예: 이진수 $110.11_2$는 과학적 표기법으로 $1.1011_2 \times 2^{+2}$로 정규화됩니다. 이 경우 지수는 $+2$입니다.
- 중요성: 이 메커니즘은 고정된 수의 비트(예: 32비트 단정밀도)를 사용하는 기계가 고정 소수점 또는 정수 형식이 달성할 수 있는 것보다 훨씬 더 넓은 범위를 포괄할 수 있도록 허용합니다(정밀도를 희생하더라도).
근본적인 문제 (Fundamental Challenge)
- 컴퓨터 그래픽스에서 부동 소수점 인코딩은 제한된 수의 비트를 사용하여 미세한 소수부터 방대한 값에 이르는 넓은 범위의 숫자를 나타내는 데 사용됩니다.
- 이는 휘도 값이 종종 1.0을 초과하는 고동적 범위(HDR) 색상 데이터를 저장하는 것과 같은 작업에 매우 중요합니다.
- 근사치의 문제:
- 이 인코딩 방법은 본질적으로 근사치에 의존합니다.
- 결과적으로, 정확한 실수 0을 정확하게 표현하거나, 두 부동 소수점 값의 정확한 동등성을 안정적으로 비교하는 것이 어렵습니다.
- 이 근본적인 한계는 수치적 안정성 문제를 야기합니다.
해결 전략 (Resolution Strategy)
- 이러한 정밀도 제한은 렌더링 파이프라인 전체, 특히 광선 교차 테스트 및 깊이 비교와 같은 고정밀 연산에서 원치 않는 아티팩트 또는 논리적 오류로 이어질 수 있습니다.
- 수치적 안정성을 보장하고 견고한 렌더링 최적화를 달성하기 위한 주요 전략은 엡실론 ($\mathbf{\epsilon}$) 오프셋을 사용하는 것입니다.
- $\mathbf{\epsilon}$은 매우 작은 양의 상수(예: $10^{-4}$ 또는 $10^{-6}$)로 정의됩니다.
- 정확한 동등성 ($\mathbf{A == B}$)을 확인하는 대신,
- 알고리즘은 두 값이 “충분히 가까운지” 또는 “하나의 값이 다른 값보다 아주 약간 큰지“를 확인합니다.
- 조건부 검사:
- $\mathbf{A}$와 $\mathbf{B}$를 비교할 때, $\mathbf{A > B + \epsilon}$와 같은 조건이 사용됩니다.
- 이는 의도적으로 미세한 정밀도 오류를 허용하여, 비교가 부동 소수점 부정확성에 대해 견고하도록 보장합니다.
-
이 엡실론 오프셋의 체계적인 적용은 현대 컴퓨터 그래픽스에서 필요한 신뢰성과 성능을 달성하기 위한 필수적인 기술입니다.
Leave a comment